Circles: Diameter, Chord, Radius, Arc, Tangent

Related Pages
Circles
Tangent Of A Circle
Chords Of A Circle

The following figures show the different parts of a circle: tangent, chord, radius, diameter, minor arc, major arc, minor segment, major segment, minor sector, major sector. Scroll down the page for more examples and explanations.

 

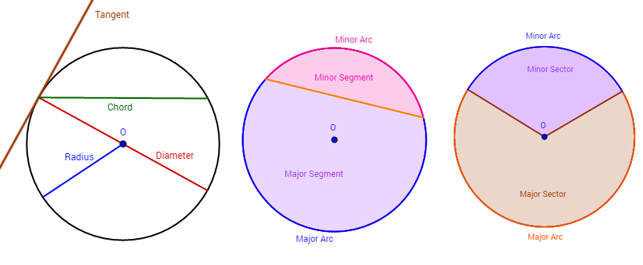
• Printable & Online Circle Worksheets

  Printable
  Circumference Worksheets
  Area of Circle Worksheets
  Area & Circumference Worksheets
  Find Radius from Circumference
  Find Radius from Area
  Find Area from Circumference or vice versa
  Circle Word Problems
  

  Online
  Circumference of Circle
  Area of Circle
  Area & Circumference of Circle
  
  Circle Problems: Circumference, Area
  Circle Word Problems 1
  Circle Word Problems 2
  
  Area of shaded regions that include circles
  Area of figures that include circles
  Area of figures that include circles
  
  Arc Length & Area of Sector (Degrees)
  Arc Length & Area of Sector (Radians)
  Convert between Radians and Degrees

Circle

In geometry, a circle is a closed curve formed by a set of points on a plane that are the same distance from its center O. That distance is known as the radius of the circle.

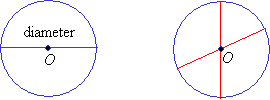
Diameter

The diameter of a circle is a line segment that passes through the center of the circle and has its endpoints on the circle. All the diameters of the same circle have the same length.

Chord

A chord is a line segment with both endpoints on the circle. The diameter is a special chord that passes through the center of the circle. The diameter would be the longest chord in the circle.

Radius

The radius of the circle is a line segment from the center of the circle to a point on the circle. The plural of radius is radii.

In the above diagram, O is the center of the circle and and   are radii of the circle. The radii of a circle are all the same length. The radius is half the length of the diameter.

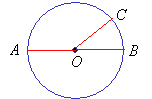
Arc

An arc is a part of a circle.

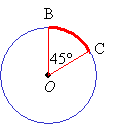
In the diagram above, the part of the circle from B to C forms an arc.

An arc can be measured in degrees.

In the circle above, arc BC is equal to the ∠BOC that is 45°.

Tangent

A tangent is a line that touches a circle at only one point. A tangent is perpendicular to the radius at the point of contact. The point of tangency is where a tangent line touches the circle.

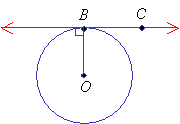
In the above diagram, the line containing the points B and C is a tangent to the circle.

It touches the circle at point B and is perpendicular to the radius . Point B is called the point of tangency.

is perpendicular to i.e.

Parts Of A Circle

The following video gives the definitions of a circle, a radius, a chord, a diameter, secant, secant line, tangent, congruent circles, concentric circles, and intersecting circles.

A secant line intersects the circle in two points.

A tangent is a line that intersects the circle at one point.

A point of tangency is where a tangent line touches or intersects the circle.

Congruent circles are circles that have the same radius but different centers.

Concentric circles are two circles that have the same center, but a different radii.

Intersecting Circles: Two circles may intersect at two points or at one point. If they intersect at one point then they can either be externally tangent or internally tangent.

Two circles that do not intersect can either have a common external tangent or common internal tangent.
In the common external tangent, the tangent does not cross between the two circles.
In the common internal tangent, the tangent crosses between the two circles.

• Show Video Lesson

Parts Of A Circle, Including Radius, Chord, Diameter, Central Angle, Arc, And Sector

• Show Video Lesson

Check out our most popular games!

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.