Pairs Of Lines
Related Pages
More Geometry Lessons
In these lessons, we will learn how pairs of lines can relate to each other in four different ways:
These concepts are useful for understanding and solving various geometry problems.
In a two-dimensional plane, pairs of lines can relate to each other in different ways:
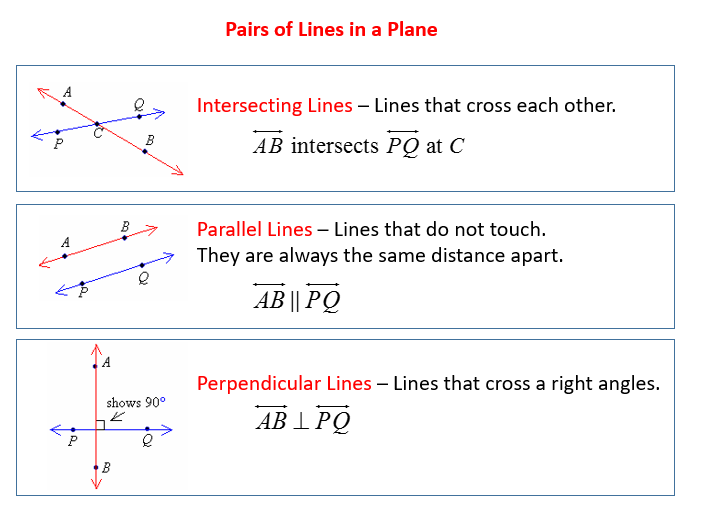
Intersecting Lines
Intersecting lines are lines cross at exactly one point. When two lines intersect, they form vertically opposite angles (which are equal).
Parallel Lines
Parallel lines are lines that never meet or intersect. They are always the same distance apart and have identical slopes in coordinate geometry.
\(\overleftrightarrow{AB}\parallel \overleftrightarrow {PQ}\) indicates that line AB is parallel to line PQ.
Perpendicular Lines
Perpendicular lines are lines that intersect at one point and form a 90° angle.
\(\overleftrightarrow{AB}\bot \overleftrightarrow {PQ}\) indicates that line AB is perpendicular to line PQ.
The following diagrams show examples of Intersecting Lines, Parallel Lines and Perpendicular Lines. Scroll down the page for more examples and solutions.
Geometry Worksheets
Practice with the following worksheets.
Printable & Online Geometry Worksheets
Videos
The following video gives a definition of intersecting lines.
The following video gives a definition of parallel lines.
Parallel lines are coplanar lines that do not intersect.
The following video gives a definition of perpendicular lines.
Parallel, Perpendicular & Intersecting Lines Song
Song to help you remember what are parallel, perpendicular and intersecting lines.
Parallel lines never meet;
Intersecting lines make v’s;
Perpendicular lines meet at 90 degrees;
Put your hands in the air with me!!
Skew Lines
The above relationships between lines take place on the same plane.
However, skew lines only happen in 3D space.
Skew lines never intersect because they are not on the same plane.
Skew lines are difficult to draw because they exist in the three
dimensional space. Lets consider a cube.
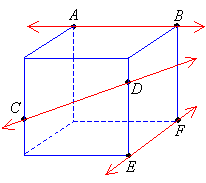 |
Imagine the lines \(\overleftrightarrow{AB}\) and \(\overleftrightarrow{EF}\) running
along the edges of a cube as shown, and line \(\overleftrightarrow{CD}\)
running on the front surface of the cube. These lines are in different planes and will never intersect. |
Videos
The following video gives a definition of skew lines.
Difference between parallel lines and skew lines.
Parallel lines are two coplanar lines that never intersect.
Skew lines are lines that are not coplanar and can never intersect.
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.