Basic Geometry Concepts

Basic Geometry
Geometric Terms	Fundamental Concepts of Geometry	Angles
Geometric Theorems	Geometry Worksheets	Math Worksheets

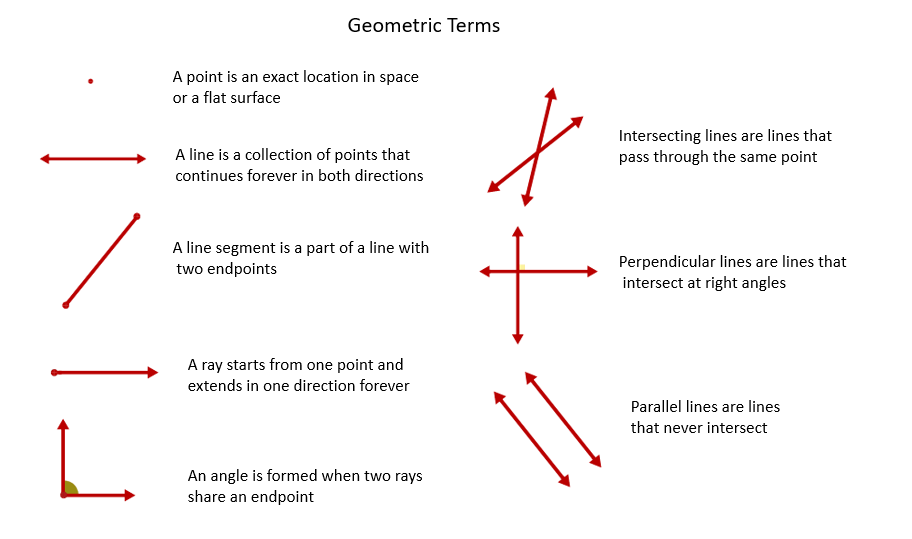
Geometric Terms

The following table gives some geometry concepts, words and notations. Scroll down the page for examples, explanations and solutions.

 

Points

We may think of a point as a "dot" on a piece of paper or the pinpoint on a board. In geometry, we usually identify this point with a number or letter. A point has no length, width, or height - it just specifies an exact location. It is zero-dimensional.

Every point needs a name. To name a point, we can use a single capital letter. The following is a diagram of points A, B, and M:

 

Lines

We can use a line to connect two points on a sheet of paper. A line is one-dimensional. That is, a line has length, but no width or height. In geometry, a line is perfectly straight and extends forever in both directions. A line is uniquely determined by two points.

Lines need names just like points do, so that we can refer to them easily. To name a line, pick any two points on the line.

The line passing through the points A and B is denoted by

A set of points that lie on the same line are said to be collinear. Pairs of lines can form intersecting lines, parallel lines, perpendicular lines and skew lines.

Line Segments

Because the length of any line is infinite, we sometimes use parts of a line. A line segment connects two endpoints. A line segment with two endpoints A and B is denoted by .

A line segment can also be drawn as part of a line.

Midpoint

The midpoint of a segment divides the segment into two segments of equal length. The diagram below shows the midpoint M of the line segment . Since M is the midpoint, we know that the lengths AM = MB.

Rays

A ray is part of a line that extends without end in one direction. It starts from one endpoint and extends forever in one direction.

A ray starting from point A and passing through B is denoted by

Planes

Planes are two-dimensional. A plane has length and width, but no height, and extends infinitely on all sides. Planes are thought of as flat surfaces, like a tabletop. A plane is made up of an infinite amount of lines. Two-dimensional figures are called plane figures.

All the points and lines that lie on the same plane are said to be coplanar.

A plane.

Space

Space is the set of all points in the three dimensions - length, width and height. It is made up of an infinite number of planes. Figures in space are called solids.

Figures in space.

Fundamental Concepts Of Geometry

This video explains and demonstrates the fundamental concepts (undefined terms) of geometry: points, lines, ray, collinear, planes, and coplanar. The basic ideas in geometry and how we represent them with symbols.

A point is an exact location in space. They are shown as dots on a plane in 2 dimensions or a dot in space in 3 dimensions. It is labeled with capital letters. It does not take up any space.

A line is a geometric figure that consists of an infinite number of points lined up straight that extend in both directions for ever (indicated by the arrows at the end). A line is identified by a lower case letter or by two points that the line passes through. There is exactly 1 line through two points. All points on the same line are called collinear. Points not on the same line are noncollinear.

Two lines (on the same plane) are either parallel or they will meet at a point of intersection.

A line segment is a part of a line with two endpoints. A line segment starts and stops at two endpoints.

A ray is part of a line with one endpoint and extends in one direction forever.

A plane is a flat 2-dimensional surface. A plane can be identified by 3 points in the plane or by a capital letter. There is exactly 1 plane through three points. The intersection of two planes is a line.

Coplanar points are points in one plane.

• Show Video Lesson

How To Measure Angles And Types Of Angles

An angle consists of two rays with a common endpoint. The two rays are called the sides of the angle and the common endpoint is the vertex of the angle.

Each angle has a measure generated by the rotation about the vertex. The measure is determined by the rotation of the terminal side about the initial side. A counterclockwise rotation generates a positive angle measure. A clockwise rotation generates a negative angle measure. The units used to measure an angle are either in degrees or radians.

Angles can be classified base upon the measure: acute angle, right angle, obtuse angle, and straight angle.

If the sum of measures of two positive angles is 90°, the angles are called complementary.

If the sum of measures of two positive angles is 180°, the angles are called supplementary.

Examples:

1. Two angles are complementary. One angle measures 5x degrees and the other angle measures 4x degrees. What is the measure of each angle?
2. Two angles are supplementary. One angle measures 7x degrees and the other measures (5x + 36) degrees. What is the measure of each angle?

• Show Video Lesson

Geometric Theorems

The Opposite Angle Theorem (OAT)
When two straight lines cross, opposite angles are equal.

The Angle Sum of a Triangle Theorem
The interior angles of any triangle have a sum of 180°.

The Exterior Angle Theorem (EAT)
Any exterior angle of a triangle is equal to the sum of the opposite interior angles.

Parallel Lines Theorem (PLT)
Whenever a pair of parallel lines is cut by a transversal
a) corresponding angles are equal (PLT-F)
b) alternate angles are equal (PLT-Z)
c) interior angles have a sum of 180° (PLT-C)

• Show Video Lesson

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.