Tangents Of Circles
Here we discuss the various symmetry and angle properties of tangents to circles.
Related Pages
Tangents Of Circles And Angles
Angles In A Circle
Circles
Cyclic Quadrilaterals
In these lessons we will learn about
- Tangent To A Circle And The Point Of Tangency,
- Tangent To A Circle Theorem,
- Secant,
- Two-Tangent Theorem,
- Common Internal And External Tangents.
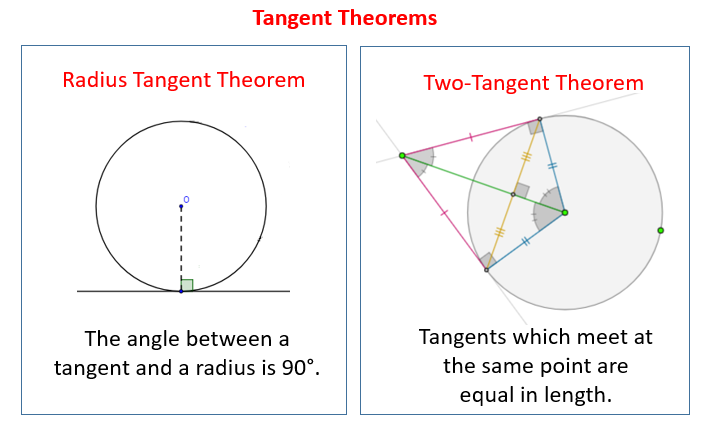
The following diagrams show the Radius Tangent Theorem and the Two-Tangent Theorem. Scroll down the page for more examples and solutions.
Tangent To A Circle
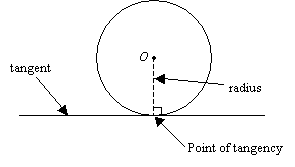
A tangent to a circle is a straight line, in the plane of the circle, which touches the circle at only one point. The point is called the point of tangency or the point of contact.
Tangent to a Circle Theorem: A tangent to a circle is perpendicular to the radius drawn to the point of tangency.
What Is The Tangent Of A Circle?
A tangent is a line in the plane of a circle that intersects the circle at one point. The point where it intersects is called the point of tangency.
How To Prove The Tangent To A Circle Theorem?
The Tangent to a Circle Theorem states that a line is tangent to a circle if and only if the line is perpendicular to the radius drawn to the point of tangency.
Secant
A straight line that cuts the circle at two distinct points is called a secant.
Example:
In the following diagram
a) state all the tangents to the circle and the point of tangency of each tangent.
b) state all the secants.
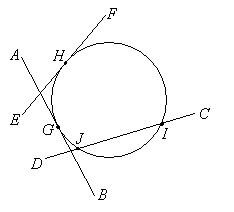
Solution:
AB is a tangent to the circle and the point of tangency is G.
CD is a secant to the circle because it has two points of contact.
EF is a tangent to the circle and the point of tangency is H.
Tangents From The Same External Point
Two-Tangent Theorem: When two segments are drawn tangent to a circle from the same point outside the circle, the segments are equal in length.
In the following diagram:
If AB and AC are two tangents to a circle centered at O, then:
- the tangents to the circle from the external point A are equal,
- OA bisects the angle BAC between the two tangents,
- OA bisects the angle BOC between the two radii to the points of contact,
- triangle AOB and triangle AOC are congruent right triangles.
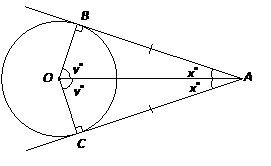
The two-tangent theorem is also called the "hat" or "ice-cream cone" theorem because it looks like a hat on the circle or an ice-cream cone.
How To Prove The Two-Tangent Theorem?
The Two-Tangent Theorem states that when two segments are drawn tangent to a circle from the same point outside the circle, the segments are congruent. (uses Two-Column Proof and CPCTC).
When Two Tangent Lines Emanate From The Same External Point
How to find an unknown angle using the two-tangent theorem?
How To Use The Two-Tangent Theorem To Solve A Geometry Problem?
How To Apply The Congruent Tangents Theorem Or Two-Tangent Theorem?
Common Internal And External Tangents
A common tangent is a line that is a tangent to each of two circles.
A common external tangent does not intersect the segment that joins the centers of the circles.
A common internal tangent intersects the segment that joins the centers of the circles.
Common Internal And External Tangents: Finding Lengths
A lesson on finding the length of common internal and external tangents.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.