Geometry: Circles
Related Pages
Angles In A Circle
Area Of A Circle
Conic Sections: Circles
A circle is a two-dimensional shape consisting of all points in a plane that are equidistant from a fixed point called the center. Circles have several important parts, each with specific properties and names.
This lesson covers the various properties of circles, the parts of a circle and the terms commonly associated with circles.
We shall learn about circles and the properties of circles.
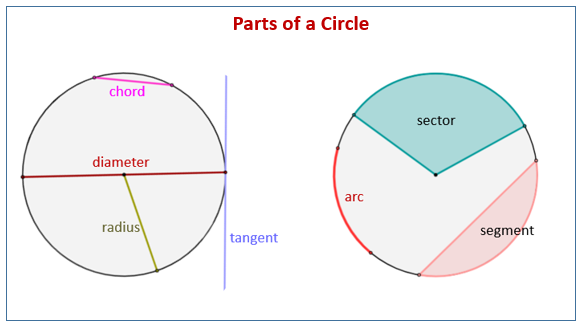
- diameter,
- chord,
- radius,
- arc,
- semicircle, minor arc, major arc,
- tangent,
- secant,
- circumference and formula,
- area and formula,
- sector and formula.
The following figures show the different parts of a circle: tangent, chord, radius, diameter, arc, segment, sector. Scroll down the page for more examples and explanations.
Geometry Worksheets
Practice your skills with the following worksheets:
Printable & Online Geometry Worksheets
Circle
In geometry, a circle is a closed curve formed by a set of points on a planeplane that are the same distance from its center O. That distance is known as the radius of the circle.
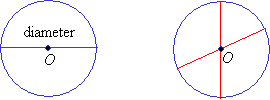
Diameter
The diameter of a circle is a line segment that passes through the center of the circle and has its endpoints on the circle. All the diameters of the same circle have the same length.
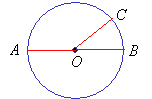
Chord & Diameter
A chord is a line segment with both endpoints on the circle. The diameter is a special chord that passes through the center of the circle. The diameter would be the longest chord in the circle.
Radius
The radius of the circle is a line segment from the center of the circle to any point on the circle. All radii (plural of radius) of a circle are equal in length.
In the above diagram, O is the center of the circle and 
and 
are radii of the circle. The radii of a circle are all the same length. The radius is half the
length of the diameter. 
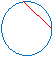
Arc
An arc is a portion of the circumference of a circle.
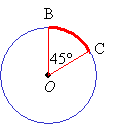
In the diagram above, the part of the circle from B to C forms an arc. It is called arc BC.
An arc can be measured in degrees. In the circle above, the measure of arc BC is equal to its central angle ∠BOC, which is 45°.
Semicircle, Minor Arc and Major Arc
A semicircle is an arc that is half a circle. A minor arc is an arc that is smaller than a semicircle. A major arc is an arc that is larger than a semicircle.
How To Identify Semicircle, Minor Arc And Major Arc?
Tangent
A tangent to a circle is a line that touches a circle at only one point. A tangent is perpendicular to the radius at the point of contact.
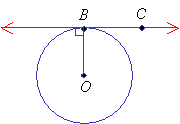
In the above diagram, the line containing the points B and C is a tangent to the circle.
It touches the circle at point B and is perpendicular to the radius
is perpendicular to i.e.
Secant
A secant is a straight line that cuts the circle at two points. A chord is the portion of a secant that lies in the circle.
Circumference
The circumference of a circle is the total distance around a circle.
Calculating the circumference of a circle involves a constant called pi with the symbol π. The value of π (pi) is approximately 3.14159265358979323846… but usually rounding to 3.142 should be sufficient. (see a mnemonic for π)
The formula for the circumference of a circle is
C = πd (see a mnemonic for this formula)
or
C = 2πr
where C is the circumference, d is the diameter and r is the radius.
If you are given the diameter then use the formula C = πd
If you are given the radius then use the formula C = 2πr
Circumference Worksheet to calculate the circumference of a circle.
Area & Circumference Worksheet to calculate the area and circumference of a circle.
Example 1: Find the circumference of the circle with a diameter of 8 inches.
Solution:
| Step 1: Write down the formula: | C = πd |
| Step 2: Plug in the value: | C = 8π |
Answer: The circumference of the circle is 8π ≈ 25.163 inches.
Example 2: Find the circumference of the circle with a radius of 5 inches.
Solution:
| Step 1: Write down the formula: | C = 2πr |
| Step 2: Plug in the value: | C = 10π |
Answer: The circumference of the circle is 10π ≈ 31.42 inches.
Explore The Relationship Between The Radius, Diameter And Circumference Of A Circle
Area
The area of a circle is the region enclosed by the circle. It is given by the formula:
A = πr2 (see a mnemonic for this formula)
where A is the area and r is the radius.
Since the formula is only given in terms of radius, remember to change from diameter to radius if necessary.
Circles Worksheet to calculate the area of a circle.
Area and Circumference Worksheet
to calculate the area and circumference of a circle.
Circle Problems Worksheet to calculate problems that involve the radius, diameter, circumference and area of circle.
Example 1: Find the area the circle with a diameter of 10 inches.
Solution:
| Step 1: Write down the formula: | A = πr2 |
| Step 2: Change diameter to radius: |  |
| Step 3: Plug in the value: | A = π52 = 25π |
Answer: The area of the circle is 25π ≈ 78.55 square inches.
Example 2: Find the area the circle with a radius of 10 inches.
Solution:
| Step 1: Write down the formula: | A = πr2 |
| Step 2: Plug in the value: | A = π102 = 100π |
Answer: The area of the circle is 100π ≈ 314.2 square inches.
How To Relate The Radius And Diameter Of A Circle With Its Area?
Sector
A sector is like a "pizza slice" of the circle. It consists of a region bounded by two radii and an arc lying between the radii. The area of a sector is a fraction of the area of the circle.
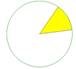
The formula to calculate the area of a sector is
How To Derive The Formula To Calculate The Area Of A Sector In A Circle?
The following video lesson explains how to find the area of a sector.
| Check out our most popular games! | ||
|---|---|---|
 Fraction Concoction |
 Fact Family Game |
 Number Bond Garden |
 Online Addition Subtraction Game |
 Penguin Solitaire |
 Sawayama Solitaire |
 Ark Solitaire |
 Eldritch Invasion |
 Shenzhen Solitaire |
Check out more Solitaire games here.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.