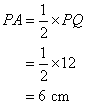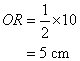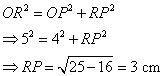Chords Of A Circle Theorems

We will learn theorems that involve chords of a circle

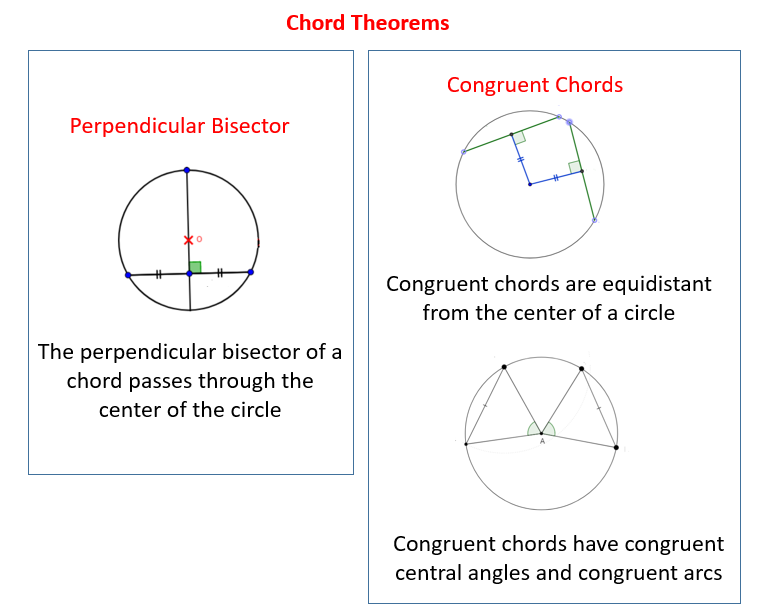
• Perpendicular bisector of a chord passes through the center of a circle.
• Congruent chords are equidistant from the center of a circle.
• If two chords in a circle are congruent, then their intercepted arcs are congruent.
• If two chords in a circle are congruent, then they determine two central angles that are congruent.

The following diagrams give a summary of some Chord Theorems: Perpendicular Bisector and Congruent Chords. Scroll down the page for examples, explanations, and solutions.

A chord is a straight line joining 2 points on the circumference of a circle.

Theorem: A radius or diameter that is perpendicular to a chord divides the chord into two equal parts and vice versa.

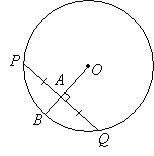
In the above circle, if the radius OB is perpendicular to the chord PQ then PA = AQ.

Converse: The perpendicular bisector of a chord passes through the center of a circle.

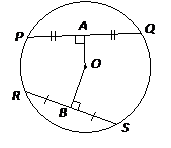
In the above circle, OA is the perpendicular bisector of the chord PQ and it passes through the center of the circle. OB is the perpendicular bisector of the chord RS and it passes through the center of the circle.

We can use this property to find the center of any given circle.

Example:
Determine the center of the following circle.

Solution:
Step 1: Draw 2 non-parallel chords

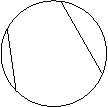
Step 2: Construct perpendicular bisectors for both the chords. The center of the circle is the point of intersection of the perpendicular bisectors.

Circles, Radius Chord Relationships, Distance From The Center To A Chord

This video shows

• how to define a chord,
• how to describe the effect of a perpendicular bisector of a chord and the distance from the center of the circle,
• that the perpendicular bisector of a chord passes through the center of the circle.

• Show Video Lesson

Theorem: Congruent Chords are equidistant from the center of a circle.

Converse: Chords equidistant from the center of a circle are congruent.

If PQ = RS then OA = OB or
If OA = OB then PQ = RS

How To Use The Chords Equidistant From The Center Of A Circle Theorem

The theorem states:

1. Chords equidistant from the center of a circle are congruent.
2. Congruent chords are equidistant from the center of a circle.

• Show Video Lesson

Theorem: If two chords in a circle are congruent then their intercepted arcs are congruent.

Converse: If two arcs are congruent then their corresponding chords are congruent.

Theorem On Chords And Arcs With An Example On How To Use The Theorem

The following video also shows the perpendicular bisector theorem.

1. If a diameter or radius is perpendicular to a chord, then it bisects the chord and its arc.
2. If two chords are congruent, then their corresponding arcs are congruent.
3. If a diameter or radius is perpendicular to a chord, then it bisects the chord and its arc.
4. In the same circle or congruent circle, two chords are congruent if and only if they are equidistant from the center.

• Show Video Lesson

Theorem: If two chords in a circle are congruent then they determine two central angles that are congruent.

This video discusses the following theorems:

1. Congruent central angles have congruent chords,
2. Congruent chords have congruent arcs,
3. Congruent arcs have congruent central angles.

• Show Video Lesson

This video describes the four properties of chords:

1. If two chords in a circle are congruent, then they determine two central angles that are congruent.
2. If two chords in a circle are congruent, then their intercepted arcs are congruent.
3. If two chords in a circle are congruent, then they are equidistant from the center of the circle.
4. The perpendicular from the center of the circle to a chord bisects the chord.

• Show Video Lesson

Example:
The figure is a circle with center O. Given PQ = 12 cm. Find the length of PA.

• Show Solution

  Solution:
  The radius OB is perpendicular to PQ. So, OB is a perpendicular bisector of PQ.

  

Example:
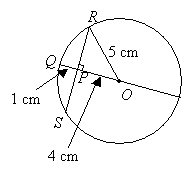
The figure is a circle with center O and diameter 10 cm. PQ = 1 cm. Find the length of RS.

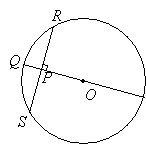
• Show Solution
  
  
  

  OP = OQ – PQ
      = 5 cm – 1 cm = 4 cm
  

  Using Pythagoras’ theorem,
  

  
  

  Since OQ is a radius that is perpendicular to the chord RS, it divides the chord into two equal parts.

  RS = 2RP = 2 × 3 = 6 cm

  If a diameter is perpendicular to a chord, then it bisects the chord and its arc.

Example:
Find the length of the radius of a circle if a chord of the circle has a length of 12 cm and is 4 cm from the center of the circle.

• Show Video Lesson

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.