Metric Math Conversion Problems
Related Pages
Introduction to the Metric System
Metric Worksheets
Measurement Games
In these lessons, we will look into some methods that can be used for metric conversion problems. The first method uses the metric table and can also be regarded as a shortcut method. The second method uses the metric staircase and the third method uses the unit fraction method. Scroll done the page for free metric worksheets.
The following diagrams show some metric conversions for lengths and weights. Scroll down the page for examples and solutions.
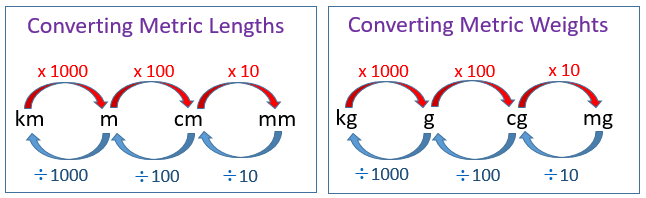
-
Metric Games/Worksheets
Metric Conversion Game
Customary Measurement Conversion GameMetric Length Conversions (km, m, cm)
Metric Mass Conversions (kg, g)
Metric Capacity Conversions (L, cL)Metric Length Word Problems
Metric Capacity Word Problems
Metric Mass Word Problems
Measurement Word Problems
Customary Measurement Word Problems
Multi-Step Measurement Word Problems
| Metric Conversion Methods | ||
|---|---|---|
| Shortcut Method | Metric Staircase | Unit Fraction |
Convert using a Metric Table or Shortcut Method
The metric system uses prefixes to denote multiple of 10.
The following table shows some common prefixes of metric units and how to convert between them.
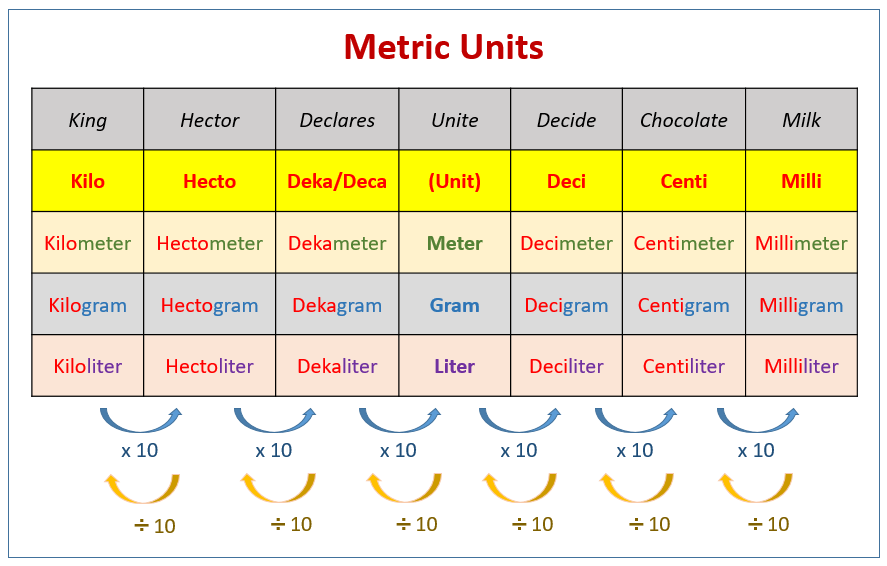
Each prefix differs by a multiple of 10 from the next prefix. When converting between the different units of measure, we look at the number of “jumps” between the prefixes of the two units and then multiply or divide by the powers of 10 accordingly (moving to the right would mean to multiply and moving to the left would mean to divide).
Example:
Convert 3 km to m
Solution:
There are 3 “jumps” to the right from kilometer to meter.
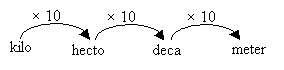
So, we multiply by 103 = 1000
3 km = 3 × 1,000 = 3,000 m
Example:
Convert 20 mm to cm
Solution:
There is 1 “jump” to the left from millimeter to centimeter
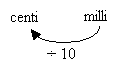
So, we divide by 10.
20 mm = 20 ÷ 10 = 2 cm
How to convert to different metric units of measure for length, capacity, and mass?
The metric system is widely used because it is based on the powers of 10. This allows for easy conversion between smaller and larger units.
The basic unit of length is the meter(m). It is just over 1 yard.
The basic unit of weight is the gram(g). One gram is the mass of 1 cubic centimeter of water.
The basic unit of capacity or volume is liter(l). A liter equals 1000 cubic centimeters.
Examples:
Complete each conversion
- 6.3km = ____ m
- 62,300cm = ___ hm
- 37,200g = ___ kg
- 1.73hg = ___ dg
- 93.7L = ___ mL
- 62,300cL = ___ kL
How to perform metric conversion using the table or shortcut method?
Use the mnemonic “King Henry Drinks Ucky Dark Chocolate Milk”
Examples:
- 0.521 mm to m
- 9501 g to kg
- 40.6 L to mL
- 1457 dm to hm
- 53.45 dag to mg
- .4 kL to mL
How to convert metric units of weight without using a calculator?
The presentation focuses on conversion between kg, g, and mg.
Imagine a 1 kilogram(kg) tablet which is made up of a 1000 smaller gram(g) tablets which is in turn made up of 1000 even smaller milligram (mg) tablets.
Big to small: multiply
Small to big: divide
How to multiply and divide by 1000 in conversion of metric units?
This tutorial explains answers to exercises in converting metric units of weight. The exercises involve multiplying and dividing without a calculator.
Metric Staircase or Ladder Method
How to use the metric staircase to convert units within the metric system?
Another method similar to the table method is to use the metric staircase. It is also called the ladder method.
Use the mnemonic “Kangaroo Helps Dingo Because Dingo Can’t Multiply”
How to use the metric staircase to convert between metric measurements?
When you go up the stairs to the left, move the decimal to the left.
When you go down the stairs to the right, move the decimal to the right.
Convert using the Unit Fraction Method
In this method, we multiply by a unit fraction in order to perform the metric conversion.
Example:
Convert 3 km to m
Solution:
![]()
Example:
Convert 20 mm to cm
Solution:
![]()
Common Metric Length Conversions Using Unit Fractions
Common Metric Weight Conversions Using Unit Fractions
Metric Measurement Worksheets
Metric Measurement Conversion
Metric Measurement Word Problems
Adding Measurements
Subtracting Measurements
Measurement Word Problems
Metric Length Worksheets
Printable & Online
Metric Length Conversions (km, m, cm)
Metric Length Word Problems (+, -)
Convert m to cm
Convert m to km and m
Adding lengths (km, m, cm, mm)
Subtracting Lengths (km, m, cm, mm)
Multiplying Lengths (km, m, cm, mm)
Dividing Lengths (km, m, cm, mm)
Interactive
Metric Length Conversion (mm, cm, m, km)
Metric Weight Worksheets
Printable & Online
Metric Mass Conversions (kg, g)
Metric Mass Word Problems (+, -)
Adding and Subtracting Weights (kg, g, mg)
Multiplying Weights (kg, g, mg)
Dividing Weights (kg, g, mg)
Interactive
Metric Weight Conversion (kg, g, mg)
Metric Area, Volume Worksheets
Metric Area Conversion
Metric Capacity Conversions (L, cL)
Metric Capacity Word Problems (+, -)
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.