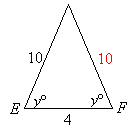SAT Practice Questions - Geometry

For more New Redesigned SAT materials, please see:
New SAT Prep
SAT Math
SAT Geometry

Share this page to Google Classroom

In addition to the questions in Heart of Algebra, Problem Solving and Data Analysis and Passport to Advanced Math, the SAT Math Test will have questions from the areas of geometry, trigonometry and complex numbers.

The following videos and solutions will show you how to solve a variety of Geometry problems for the New Redesigned SAT.

Geometry
These are some of the areas in Geometry that you will need to know for the SAT Math Test.

Lines and Angles: Lengths and midpoints, Vertical angles, Straight angles and the sum of angles about a point, Properties of parallel lines and angles formed by a transversal, Properties of perpendicular lines.

Triangles and other polygons: Right triangles, Pythagorean Triples and the Pythagorean Theorem, Properties of equilateral and isosceles triangles, Properties of 30°-60°-90° triangles and 45°-45°-90° triangles, Congruent triangles and other congruent figures, Similar triangles and other similar figures, The triangle inequality, Quadrilaterals, Regular polygons.

Circles: Radius, diameter and circumference, Measure of central angles and inscribed angles, Arc Length and area of sectors, Tangents and chords.

Solids: Area, Surface Area and Volume

Geometry Practice Test Questions And Step By Step Solutions For The New Redesigned SAT

The subsequent materials relate to the SAT before March 2016.
Try out the following Geometry Questions to help you prepare for the SAT, ACT or other similar examinations.

SAT Practice Questions - Geometry:

(Note: You may need to enable JavaScript on your browser for the hints and solutions to show properly.)

Related Pages
More Geometry Lessons

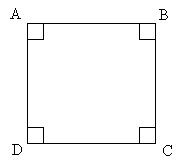
Question 1

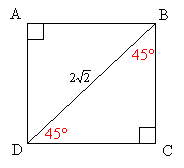
What is the area of the following square, if the length of BD is ?

          (A)
          (B)
          (C)
          (D)
          (E)

1
2
3
4
5

Show Hint

special triangles, area of square
Show Solution

Step 1: We need to find the length of the side of the square in order to get the area.
Step 2: The diagonal BD makes two 45°-45°-90° triangles with the sides of the square.
Step 3: Using the 45°-45°-90° special triangle ratio . If the hypotenuse
is then the legs must be 2. So the length of the side of the square is 2.
Step 4: Area of square = s² = 2² = 4

Answer: (D) 4

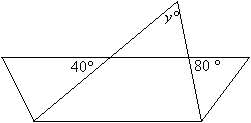
Question 2

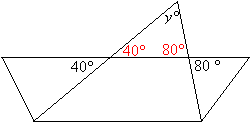
In the figure below, what is the value of y ?

          (A)
          (B)
          (C)
          (D)
          (E)

40
50
60
100
120

Show Hint

vertical angles, sum of angles in a triangle
Show Solution

Step 1: Vertical angles being equal allows us to fill in two angles in the triangle that
y° belongs to.
Step 2: Sum of angles in a triangle = 180°.
So, y° + 40° + 80° = 180°
y° + 120° = 180°
y° = 60°

Answer: (C) 60

Question 3

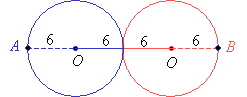
Two circles both of radii 6 have exactly one point in common. If A is a point on one circle and B is a point on the other circle, what is the maximum possible length for the line segment AB?

          (A)
          (B)
          (C)
          (D)
          (E)

12
15
18
20
24

Show Hint

radius of circle
Show Solution

Step 1: Sketch the two circles touching at one point.
Step 2: The furthest that A and B can be would be at the two ends as shown in the
above diagram.
Step 3: If the radius is 6 then the diameter is 2 × 6 = 12 and the distance from A to
B would be 2 × 12 = 24

Answer: (E) 24

Question 4

A right circular cylinder has a radius of 3 and a height of 5. Which of the following dimensions of a rectangular solid will have a volume closest to the cylinder.

          (A)
          (B)
          (C)
          (D)
          (E)

4, 5, 5
4, 5, 6
5, 5, 5
5, 5, 6
5, 6, 6

Show Hint

volume of cylinder, volume of rectangular solid
Show Solution

Step 1: Write down formula for volume of cylinder
V = πr²h
Step 2: Plug in the values
V = π × 3² × 5 = 45π**
V = 45 × 3.142* =* 141.39
Step 3: We now have to test the volume of each of the rectangular solids to find
out which is the closest to 141.39
(A) 4 × 5 × 5 = 100
(B) 4 × 5 × 6 = 120
(C) 5 × 5 × 5 = 125
(D) 5 × 5 × 6 = 150
(E) 5 × 6 × 6 = 180

Answer: (D) 5, 5, 6

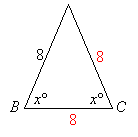
Question 5

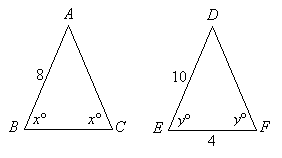
triangles
Note: Figures not drawn to scale

In the figures above, x = 60. How much more is the perimeter of triangle ABC compared with the triangle DEF.

          (A)
          (B)
          (C)
          (D)
          (E)

0
2
4
6
8

Show Hint

types of triangles, equilateral triangles, isosceles triangles
Show Solution

Note: Figures not drawn to scale Step 1: Since x = 60°, triangle ABC is an equilateral triangle with sides all equal.
The sides are all equal to 8.
Perimeter of triangle ABC = 8 + 8 + 8 = 24.
Step 2: Triangle DEF has two angles equal, so it must be an isosceles triangle.
The two equal sides will be opposite the equal angles.
So, the length of DF = length of DE = 10.
Perimeter of triangle DEF = 10 + 10 + 4 = 24.
Step 3: Subtract the two perimeters.
24 – 24 = 0

Answer to Question 5: (A) 0

SAT Practice Questions - Geometry:

SAT Geometry Problem
This is an SAT style Geometry problem that requires good thinking to solve it. It goes beyond knowing the mathematical formulas.
In the figure below, arc SBT is one quarter of a circle with center R and radius 7. The length plus the width of the rectangle ABCR is 9.5. Find the perimeter of the shaded region.

Show Video Lesson

GMAT Math Problem 03 (Geometry- Angles)
Geometry challenge problem from past GMAT exam.

Show Video Lesson

SAT Math Practice Question - Shaded Area Geometry

Show Video Lesson

What is f(2) for the graph of f(x) below?

Show Video Lesson

SAT Math Practice Question - Geometry with Equilateral Triangle
In the figure WXYT is a square and triangle TYZ is equilateral. If WXYT has area 1, what is the area of triangle TYZ?
Hint: The angles in an equilateral triangle are 60°.

Show Video Lesson

In the following diagram, AD is parallel to BC, AC = 13, BC = 5, BD = 15. What is the length of AD?

Show Video Lesson

SAT Math Practice Question- Coordinate Geometry and Recognizing Triangles
In the figure line OB is rotated counterclockwise, keeping point O fixed. What will be the coordinates of point B when it meets the y-axis?

Show Video Lesson

This video explains how to solve SAT math angle problems. Angle basics discussed include straight angles, vertical angles, angles formed when a line crosses two parallel lines, and the sum of angles in triangles and other polygons. This video contains examples from the official SAT practice tests.

Show Video Lesson

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.