Geometry: Polygons

Related Topics:
More Lessons for Geometry

Math Worksheets

What are Polygons?

Polygons are two-dimensional many-sided figures on a plane, with sides that are line segments. Some examples are: triangles, quadrilaterals, pentagons (5-sided) and hexagons (6-sided).

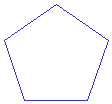
Pentagon (5-sided polygon)

A regular polygon is a polygon with equal sides and equal angles.

Regular polygon

How to find the sum of angles in a polygon?

Sum of Angles in a Triangle

The sum of angles in a triangle is 180°.

For the sum of angles of other polygons, we can either divide the polygons into triangles or use a formula.

Dividing polygons into triangles

For the other polygons, we can figure out the sum of angles by dividing the polygons into triangles. Any polygon can be separated into triangles by drawing all the diagonals that can be drawn from one single vertex.

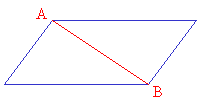
In the quadrilateral shown below, we can draw only one diagonal from vertex A to vertex B. So, a quadrilateral can be separated into two triangles.

The sum of angles in a triangle is 180°. Since a quadrilateral is made up of two triangles the sum of its angles would be 180° × 2 = 360°

The sum of angles in a quadrilateral is 360°

Formula for the sum of angles

We can also use a formula to find the sum of the interior angles of any polygon.

If n is the number of sides of the polygon then,

sum of angles = (n - 2)180°

Example 1:

Find the sum of the interior angles of a hexagon (6-sided polygon)

Solution:

Step 1: Write down the formula (n - 2)180°

Step 2: Plug in the values(6 - 2)180° = (4)180° = 720°

Answer: The sum of the interior angles of a hexagon (6-sided) is 720°.

The following video shows a problem involving the sum of interior angles of a polygon. Sum of interior angles of a polygon
Showing a generalized way to find the sum of the interior angles of any polygon