Geometry: Special Right Triangles

Recognizing Special Right Triangles

“Special right triangles” are right-angled triangles with specific angle measures that result in unique, consistent ratios between their side lengths. These ratios make calculations much faster and provide exact values without needing a calculator or complex trigonometry every time.

There are two primary types of special right triangles you’ll encounter in geometry and trigonometry:
The 45-45-90 Triangle
The 30-60-90 Triangle

Pythagorean Triples
A Pythagorean triple consists of three positive integers (a,b,c) that satisfy the Pythagorean theorem for a right triangle:
a² + b² = c²
where c is the hypotenuse, a and b are the legs.

Some examples of Pythagorean Triples are (3, 4, 5), (5, 12, 13), (8, 15, 17) and their multiples. Recognizing these Triples will allow you to find the length of the sides without using the Pythagorean Theorem formula.

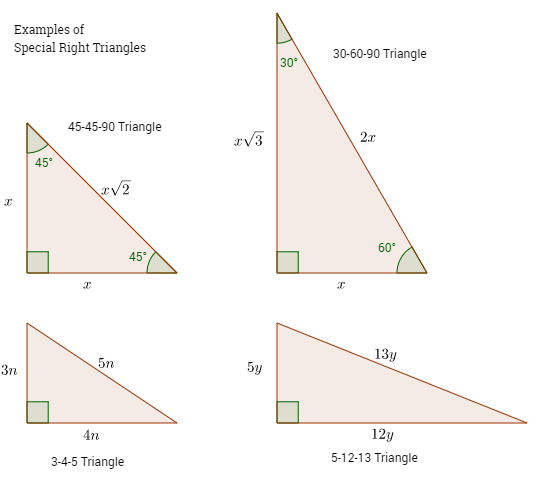
The following figures show some examples of special right triangles and Pythagorean Triples. Scroll down the page if you need more explanations about special right triangles, Pythagorean triples, videos and worksheets.

Printable & Online Geometry Worksheets
Printable & Online Trigonometry Worksheets

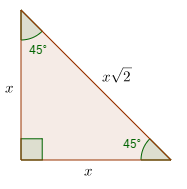
What is a 45°-45°-90° Triangle?

A 45°-45°-90° triangle is a special right triangle whose angles are 45°, 45° and 90°. The lengths of the sides of a 45°-45°-90° triangle are in the ratio of 1 : 1 : √2.

A right triangle with two sides of equal lengths must be a 45°-45°-90° triangle. It is an isosceles right triangle.

You can also recognize a 45°-45°-90° triangle by the angles. A right triangle with a 45° angle must be a 45°-45°-90° special right triangle.

Side1 : Side2 : Hypotenuse = x : x : x√2

Example 1:
Find the length of the hypotenuse of a right triangle if the lengths of the other two sides are both 3 inches.

Solution:
Step 1: This is a right triangle with two equal sides so it must be a 45°-45°-90° triangle.

Step 2: You are given that the both the sides are 3. If the first and second value of the ratio x:x:x√2 is 3 then the length of the third side is 3√2.

Answer: The length of the hypotenuse is 3√2 inches.

Example 2:
Find the lengths of the other two sides of a right triangle if the length of the hypotenuse is 4√2 inches and one of the angles is 45°.

Solution:
Step 1: This is a right triangle with a 45°-45°-90° triangle.

Step 2:
You are given that the hypotenuse is 4√2. If the third value of the ratio n:n:n√2 is 4√2 then the lengths of the other two sides must 4.

Answer: The lengths of the two sides are both 4 inches.

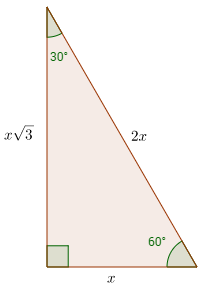
What is a 30°-60°-90° Triangle?

Another type of special right triangles is the 30°-60°-90° triangle. This is right triangle whose angles are 30°-60°-90°. The lengths of the sides of a 30°-60°-90° triangle are in the ratio of 1 : √3 : 2.

You can also recognize a 30°-60°-90° triangle by the angles. As long as you know that one of the angles in the right-angle triangle is either 30° or 60° then it must be a 30°-60°-90° special right triangle. A right triangle with a 30° angle or 60° angle must be a 30°-60°-90° special right triangle.

Side1 : Side2 : Hypotenuse = x : x√3 : 2x

Example 1:
Find the length of the hypotenuse of a right triangle if the lengths of the other two sides are 4 inches and 4√3 inches.

Solution:
Step 1: Test the ratio of the lengths to see if it fits the n:n√2:2n ratio.
4:4√3:? = x:x√3:2x

Step 2: Yes, it is a 30°-60°-90° triangle for x = 4

Step 3: Calculate the third side.
2x = 2 × 4 = 8

Answer: The length of the hypotenuse is 8 inches.

Example 2:
Find the lengths of the other two sides of a right triangle if the length of the hypotenuse is 8 inches and one of the angles is 30°.

Solution:
This is a right triangle with a 30° angle so it must be a 30°-60°-90° triangle.

You are given that the hypotenuse is 8.
Substituting 8 into the third value of the ratio x:x√3:2x, we get that 2x = 8 ⇒ x = 4.

Substituting x = 4 into the first and second value of the ratio we get that the other two sides are 4 and 4√3.

Answer: The lengths of the two sides are 4 inches and 4√3 inches.

Special Triangles - Important Angles - 30°, 45°, 60°
45°-45°-90° Triangles, 30°-60°-90° Triangles.

• Show Video Lesson

Basic triangles you should know
The triangles are classified by side and by angle.

In this video you will learn:

1. 3-4-5 triangles and similar triangles.
2. 5-12-13 triangles and similar triangles.
3. 45-45-90 right triangles.
4. 30-60-90 triangles.
5. equilateral triangles.
6. relationship between equilateral and 30-60-90 triangles.

• Show Video Lesson

How to Solve Special Right Triangles?
When solving special right triangles, remember that a 30-60-90 triangle has a hypotenuse twice as long as one of the sides, and a 45-45-90 triangle has two equal sides.

• Show Video Lesson

Special Right Triangles in Geometry
45-45-90 and 30-60-90 degree triangles.

Discuss two special right triangles, how to derive the formulas to find the lengths of the sides of the triangles by knowing the length of one side, and a few examples using them.

• Show Video Lesson

What are Pythagorean Triples?
Any group of 3 integer values that satisfies the equation: a² + b² = c² is called a Pythagorean Triple. Any triangle that has sides that form a Pythagorean Triple must be a right triangle. Some examples of Pythagorean Triple triangles are: 3-4-5 Triangles and 5-12-13 Triangles.

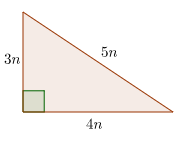
What is a 3-4-5 Triangle?
A 3-4-5 triangle is right triangle whose lengths are in the ratio of 3:4:5. When you are given the lengths of two sides of a right triangle, check the ratio of the lengths to see if it fits the 3:4:5 ratio.

Side1 : Side2 : Hypotenuse = 3n : 4n : 5n

Example 1:
Find the length of the hypotenuse of a right triangle if the lengths of the other two sides are 6 inches and 8 inches.

Solution:
Step 1: Test the ratio of the lengths to see if it fits the 3n : 4n : 5n ratio.

6 : 8 : ? = 3(2) : 4(2) : ?

Step 2: Yes, it is a 3-4-5 triangle for n = 2.

Step 3: Calculate the third side.

5n = 5 × 2 = 10

Answer: The length of the hypotenuse is 10 inches.

Example 2:
Find the length of one side of a right triangle if the length of the hypotenuse is 15 inches and the length of the other side is 12 inches.

Solution:
Step 1: Test the ratio of the lengths to see if it fits the 3n : 4n : 5n ratio.

? : 12 : 15 = ? : 4(3) : 5(3)

Step 2: Yes, it is a 3-4-5 triangle for n = 3.

Step 3: Calculate the third side.

3n = 3 × 3 = 9

Answer: The length of the side is 9 inches.

What is a 5-12-13 Triangle?
A 5-12-13 triangle is a right-angled triangle whose lengths are in the ratio of 5:12:13. It is another example of a special right triangle.

Example:

3-4-5 and 5-12-13 are examples of the Pythagorean Triple. They are usually written as (3, 4, 5) and (5, 12, 13). In general, a Pythagorean triple consists of three positive integers such that a² + b² = c². Two other commonly used Pythagorean Triples are (8, 15, 17) and (7, 24, 25)

Concepts and patterns of Pythagorean triples

• Show Video Lesson

Examples and families of Pythagorean Triples

• Show Video Lesson

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.