Geometry: Area of Polygons
In these lessons, we will learn how to use formulas to find the area of polygons: square, rectangle, parallelogram, triangle, equilateral triangle, rhombus, kite, trapezoid and the area of any regular polygon.
Related Pages
Polygons
Area Of Polygons - Composition and Decomposition
Area Of Circles
More Geometry Lessons
Area Of Polygons - Formulas
The area of a polygon measures the size of the region enclosed by the polygon. It is measured in units squared.
The following table gives the formulas for the area of polygons. Scroll down the page if you need more explanations about the formulas, how to use them as well as worksheets.
Area Of A Square
The area of a square is equal to the length of one side squared.
Area of a square = s2
Area Of A Rectangle
The area of a rectangle" is equal to the product of the length of its base and the length of its height. Sometimes, the height is called the "altitude". We can also call the longer side the "length" and the shorter side the "width"
Area of a rectangle = lw
Worksheet 1, Worksheet 2, Worksheet 3 to calculate the area and perimeter of rectangles.
Area Of A Parallelogram
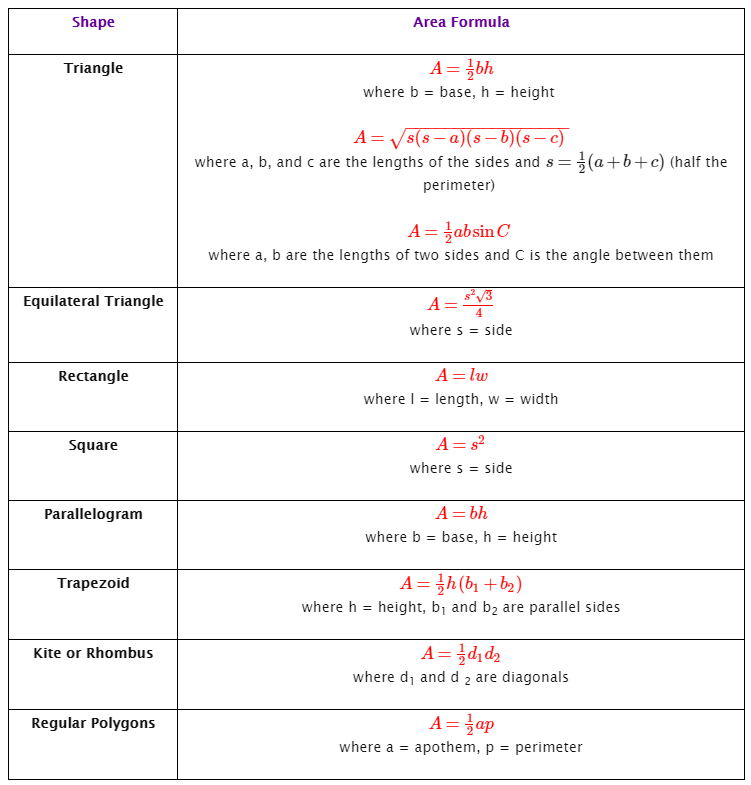
To get the area of a parallelogram, we first draw a perpendicular line segment from one corner of the parallelogram to the opposite side. This is the height (h) of the parallelogram. The area of a parallelogram is equal to the product of its length and height. (Remember to always use the perpendicular height.)
Area of a parallelogram = lh
You may notice that lh is also the area of a rectangle with dimensions l and h. The diagram below will explain why. If we cut out the triangle ABC and add it to the other side (triangle DEF), you will have a rectangle with dimensions l and h that has the same area as the original parallelogram.
Worksheet to calculate the area of parallelograms.
Area Of A Triangle
To get the area of a triangle, we first choose one of the sides to be the base (b). Then we draw a perpendicular line segment from a vertex of the triangle to the base. This is the height (h) of the triangle. The area of a triangle is equal to half the product of the base and the height.
There are also other formulas for the area of a triangle. More examples, formulas and videos for area of triangles
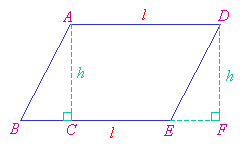
Area Of A Rhombus
We can obtain the area of a rhombus, given the lengths of its diagonals.
If the lengths of the diagonals are a and b, then area of the rhombus is equal to half the product of the diagonals.
Area of rhombus = 
If you are given the length of one side (s) and the perpendicular height (h) from one side to the vertex then the area of the rhombus is equal to the product of the side and height.
The area of the rhombus is given by the formula:
Area of rhombus = sh
This formula for the area of a rhombus is similar to the area formula for a parallelogram.
Area Of A Kite
The area of a kite uses the same formula as the area of a rhombus. The area of a kite is equal to half the product of the diagonals.
Area of kite =
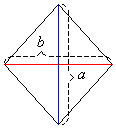
Area Of A Trapezoid
a is parallel to b
To get the area of a trapezoid, we sum the length of the parallel sides and multiply that with half of the height. Remember that the height needs to be perpendicular to the parallel sides.
Worksheet to calculate area of polygons.
The following video gives formulas and examples to find the area of squares, rectangles, triangles, parallelograms, and trapezoids. It also explains the difference between base and height.
How to derive the area formula of a kite and a rhombus based on the rectangle formula?
How to calculate the area of a rectangle using diagonal lengths?
Area Of Any Regular Polygon
A regular polygon is a polygon where all the sides are the same length and all the angles are equal.
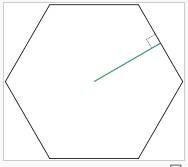
How to find the area of a regular polygon?
The apothem of a regular polygon is a line segment from the center of the polygon to the midpoint of one of its sides. The area of any regular polygon is equal to half of the product of the perimeter and the apothem.
Area of regular polygon = 
where p is the perimeter and a is the apothem.
How to use the formula to find the area of any regular polygon?
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.