Pairs Of Angles

Pairs of angles are formed when two lines intersect or when a transversal line crosses two or more other lines. Understanding these pairs is crucial in geometry. Here are the common types of angle pairs.

The following diagrams show how vertical angles, corresponding angles, and alternate angles are formed. Scroll down the page for more examples and solutions.

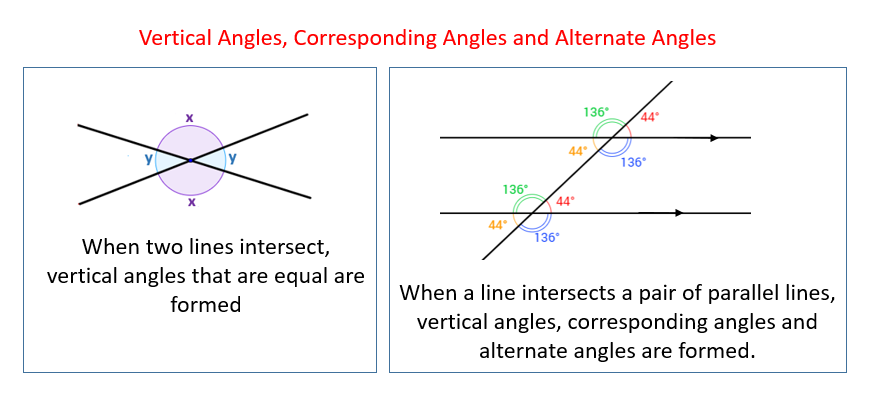
• Printable & Online Angle Worksheets

  Printable
  Types of Angles (Acute, Obtuse, Right)
  Angles on a Straight Line
  Vertical Angles
  Complementary Angles
  Supplementary Angles
  Complementary & Supplementary Angles
  Angles at a Point
  Calculate Adjacent Angles
  

  Angle Word Problems
  

  Online
  Types of Angles
  Angles in a Straight Line
  Angles at a Point
  Complementary Angles
  Supplementary Angles

Complementary Angles

Two angles are called complementary angles if the sum of their degree measurements equals 90 degrees (right angle). One of the complementary angles is said to be the complement of the other.

The two angles do not need to be together or adjacent. They just need to add up to 90 degrees. If the two complementary angles are adjacent then they will form a right angle.

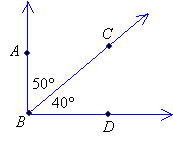
∠ABC is the complement of ∠CBD

Supplementary Angles

Two angles are called supplementary angles if the sum of their degree measurements equals 180 degrees (straight line). One of the supplementary angles is said to be the supplement of the other.

The two angles do not need to be together or adjacent. They just need to add up to 180 degrees. If the two supplementary angles are adjacent then they will form a straight line.

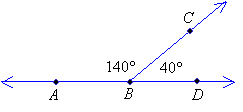
∠ABC is the supplement of ∠CBD

Vertical Angles

Two pairs of angles are formed by two intersecting lines. Vertical angles are opposite angles in such an intersection. Vertical angles are equal to each other.

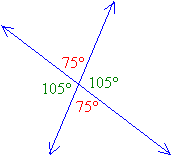
Very often math questions will require you to work out the values of angles given in diagrams by applying the relationships between the pairs of angles.

Example 1:
Given the diagram below, determine the values of the angles x, y and z.

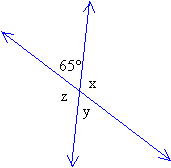
Solution:
Step 1: x is a supplement of 65°.
Therefore, x + 65° = 180° ⇒ x = 180° – 65° = 115°

Step 2: z and 115° are vertical angles.
Therefore, z = 115°

Step 3: y and 65° are vertical angles.
Therefore, y = 65°

Answer: x = 115°, y = 65° and z = 115°

How To Use Complementary, Supplementary, And Vertical Angle Pairs Property To Solve For X?

• Show Video Lesson

Alternate Interior Angles

When a line intersects a pair of parallel lines alternate interior angles are formed. Alternate interior angles are equal to each other.

 

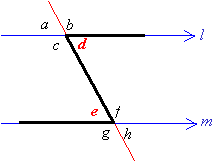
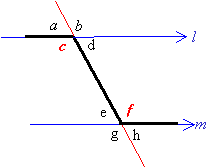
One way to find the alternate interior angles is to draw a zigzag line on the diagram. In the above diagrams, d and e are alternate interior angles. Similarly, c and f are also alternate interior angles.

Example 1:
Given the diagram below, determine the values of the angles b, c, d, e, f, g and h.

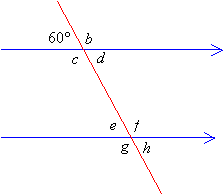
Solution:
Step 1: b is a supplement of 60°.
Therefore, b + 60° =180° ⇒ b = 180° – 60° = 120°

Step 2: b and c are vertical angles.
Therefore, c = b = 120°

Step 3: d and 60° are vertical angles.
Therefore, d = 60°

Step 4: d and e are alternate interior angles.
Therefore, e = d = 60°

Step 5: f and e are supplementary angles.
Therefore, f + 60° =180° ⇒ f = 180° – 60° = 120°

Step 6: g and f are vertical angles.
Therefore, g = f = 120°

Step 7: h and e are vertical angles.
Therefore, h = e = 60°

Answer: b = 120°, c = 120°, d = 60°, e = 60°, f = 120°, g = 120°and h = 60°

From the above example, you may notice that either an angle is 60° or it is 120°. Actually, all the small angles are 60° and all the big angles are 120°. In general, the diagram will be as shown below. The small and big pair of angles are supplementary (i.e. small + big = 180°). Therefore, given any one angle you would be able to work out the values of all the other angles.

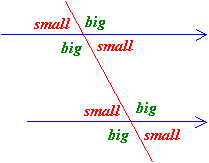
How To Find Alternate Interior Angles?

If two parallel lines are intersected by a transversal then alternate interior angles are congruent.

• Show Video Lesson

Alternate Exterior Angles

One way to remember alternate exterior angles is that they are the vertical angles of the alternate interior angles. Alternate exterior anglesare equal to one another.

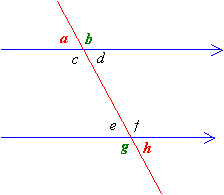
∠a and ∠h are alternate exterior angles and they are equal to one another.

∠b and ∠g are alternate exterior angles and they are equal to one another.

How To Find Alternate Exterior Angles?
If two parallel lines are intersected by a transversal then alternate exterior angles are congruent.

• Show Video Lesson

Corresponding Angles

When a line intersects a pair of parallel lines corresponding angles are formed. Corresponding angles are equal to each other.

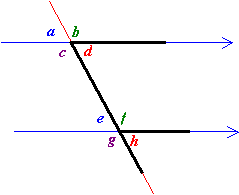
One way to find the corresponding angles is to draw a letter F on the diagram. The F can also be facing backwards.

In the above diagram, ∠d and ∠h are corresponding angles.

There many other corresponding pairs of angles in the diagram:
∠b and ∠f;
∠c and ∠g;
∠a and ∠e.

How To Find Congruent Corresponding Angles?

• Show Video Lesson

Adjacent Angles

When two angles are next to one another, they are called adjacent angles. Adjacent angles share a common side and a common vertex.

Example:
∠x and ∠y are adjacent angles.

How To Find Adjacent Angles?

• Show Video Lesson

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.