Geometry: Types Of Triangles
Related Pages
Classifying Triangles
Special Right Triangles
Area Of Triangles
More Geometry Lessons
In these lessons, we will learn to
- classify triangles by angles: Right Triangles, Acute Triangles, Obtuse Triangles, Oblique Triangles.
- classify triangles by length of sides: Equilateral Triangles, Isosceles Triangles, Scalene Triangles.
- solve some problems involving angles and sides of triangles.
Triangles
This lesson reviews the common types of triangles in geometry.
Triangles are three-sided shapes that lie in one plane.
Triangles are polygons that have three sides, three vertices and three angles.
The sum of all the angles in any triangle is 180°.
Classifying Triangles
Triangles can be classified according to the size of its angles. Some examples are right triangles, acute triangles and obtuse triangles.
The lengths of the sides of triangles is another common classification for types of triangles. Some examples are equilateral triangles, isosceles triangles and scalene triangles.
The following figures show the different types of triangles. Scroll down the page if you need more explanations and examples of each type of triangle and how to solve problems involving them.
Triangles Classified By Their Angles
Right Triangles
A right triangle is a triangle with a right angle (i.e. 90°).
You may have noticed that the side opposite the right angle is always the triangle’s longest side. It is called the hypotenuse of the triangle. The other two sides are called the legs. The lengths of the sides of a right triangle are related by the Pythagorean Theorem. There are also special right triangles.
Example 1:
A right triangle has one other angle that is 35°. What is the size of the third angle?
Solution:
Step 1: A right triangle has one angle = 90°. Sum of known angles
is 90° + 35° = 125°.
Step 2: The sum of all the angles in any triangle is 180°.
Subtract sum of known angles from 180°. 180° − 125° = 55°
Answer: The size of the third angle is 55°
Acute Triangles
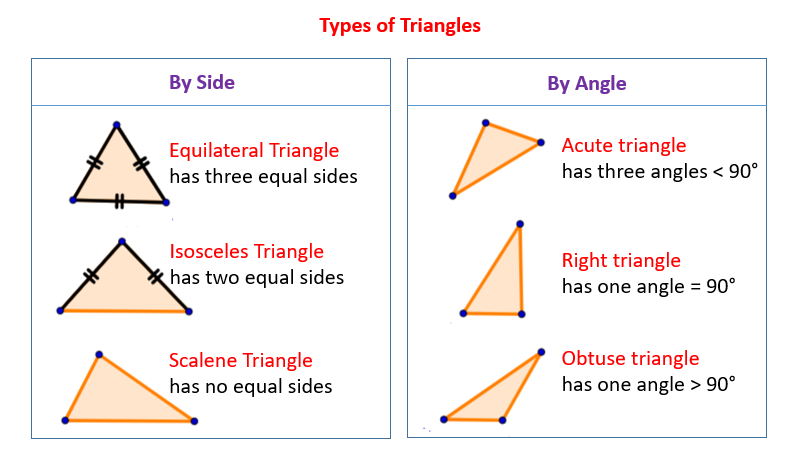
An acute triangle is a triangle whose angles are all acute (i.e. less than 90°). In the acute triangle shown below, ∠a, ∠b and ∠c are all acute angles.
Example 1:
A triangle has angles 46°, 63° and 71°. What type of triangle is this?
Answer: Since all its angles are less than 90°, it is an acute triangle.
Obtuse Triangles
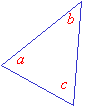
An obtuse triangle has one obtuse angle (i.e. greater than 90°). The longest side is always opposite the obtuse angle. In the obtuse triangle shown below, ∠a is the obtuse angle.
Example 1:
Is it possible for a triangle to have more than one obtuse angle?
Solution:
Step 1: Let the angles of the triangle be a, b and c.
Let a be the obtuse angle.
Step 2: The sum of all the angles in any triangle is 180°.
a + b + c = 180°.
If a > 90° then b + c must be less than 90°. Therefore, b and c must be acute angles.
Answer: No, a triangle can only have one obtuse angle.
Oblique Triangles
An oblique triangle is any triangle that is NOT a right triangle. Acute triangles and obtuse triangles are oblique triangles.
Triangles Classified By Their Sides
Besides classifying types of triangles according to the size of its angles as above: right triangles, acute triangles and obtuse triangles; triangles can also be classified according to the lengths of its sides. Some examples are equilateral triangles, isosceles triangles and scalene triangles.
Equilateral Triangles
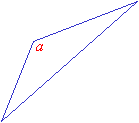
An equilateral triangle has all three sides equal in length. Its three angles are also equal and they are each 60°. An equilateral triangle is also an equiangular triangle since all its angles are equal.
Example 1:
An equilateral triangle has one side that measures 5 in. What is the size of the angle opposite that side?
Solution:
Step 1: Since it is an equilateral triangle all its angles would
be 60°. The size of the angle does not depend on the length of the side.
Answer: The size of the angle is 60°.
Isosceles Triangles
An isosceles triangle has two sides of equal length. The angles opposite the equal sides are also equal.
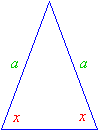
Example 1:
An isosceles triangle has one angle of 96°. What are the sizes of the other two angles?
Solution:
Step 1: Since it is an isosceles triangle it will have two equal
angles. The given 96° angle cannot be one of the equal pair because a triangle cannot have two obtuse
angles. (Refer to obtuse triangle above).
Step 2: Let x be one of the two equal angles. The sum of all the
angles in any triangle is 180°.
x + x + 96° = 180° ⇒ 2_x_ = 84° ⇒ x = 42°
Answer: The sizes of the other two angles are 42° each.
Example 2:
A right triangle has one other angle that is 45°. Besides being right triangle what type of triangle
is this?
Solution:
Step 1: Since it is right triangle it will have one 90° angle.
The other angle is given as 45°.
Step 2: Let x be third angle. The sum of all the angles in any
triangle is 180°.
x + 90° + 45° = 180° ⇒ x = 45°
Step 3: Two of the angles are equal which means that it is an
isosceles triangle.
Answer: It is also an isosceles triangle.
Scalene Triangles
A scalene triangle has no sides of equal length. Its angles are also all different in size.
Quick Recap On Types Of Triangles
We’ve looked at classifying types of triangles according to the size of its angles: right triangles, acute triangles and obtuse triangles; and also covered types of triangles according to the length of its sides: equilateral triangles, isosceles triangles and scalene triangles.
We can also name triangles according to both their angles and sides:
Acute isosceles triangles, right isosceles triangles, obtuse isosceles triangles.
Acute scalene triangles, right scalene triangles, obtuse scalene triangles
Videos
Types of Triangles - Equilateral, Isosceles, Scalene
Triangle classifications - scalene, isosceles, equilateral, acute, obtuse, right, and equiangular.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.