Variance
In these lessons, we will learn
- Population Variance
- Sample Variance
- Alternate Formulas or Computational Formulas for Variance
Related Pages
Central Tendency & Variance
Standard Deviation
Statistics Lectures - 5: Variance & Percentiles
ANOVA Test
More Statistics Lessons
The following diagrams give the population variance formula and the sample variance formula. Scroll down the page for more examples and solutions on how to use the variance formulas.

Population Variance
The variance is the average of the squared deviations about the mean for a set of numbers. The population variance is denoted by σ2. It is given by the formula:
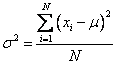
The capital Greek letter sigma 𝚺 is commonly used in mathematics to represent a summation of all the numbers in a grouping.
N is the number of terms in the population.
How To Calculate The Variance Of A Population?
Variance as a measure of, on average, how far the data points in a population are from the population mean.
Population Variance And Standard Deviation
How to calculate the variance and standard deviation?
Sample Variance
The sample variance is denoted by s2. The main use for sample variances is as estimators of population variances. The computation of the sample variance differs slightly from computation of the population variance. The sample variance uses n – 1 in the denominator instead of n because using n in the denominator of a sample variance results in a statistic that tends to underestimate the population variance. (This is further explained in the video below)
The formula for sample variance is:
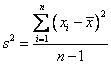
How to use the variance of a sample to estimate the variance of a population?
What is the formula of sample variance and how to finding the sample variance?
Alternate Formulas Or Computational Formulas For Variance
Sometimes, books may give different formulas for variance.
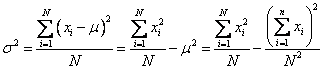
We will now show how to derive these different formulas for variance.

How to derive the different alternate formulas for variance?
How to find the sample standard deviation using the computation formula?
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.