Solid Geometry
Related Pages
Surface Area Formulas
Volume Formulas
More Geometry Lessons
In these lessons, we will look at the geometric properties of solid shapes (3D shapes), such as cubes, cuboids, prisms, cylinders, cones, pyramids and spheres. We will look into the formulas for the volume and surface area of the solid shapes and how to use them. You can also use the worksheets to practice calculating the volumes and surface areas of the 3D shapes.
What Is Solid Geometry?
Solid geometry is concerned with three-dimensional shapes. Some examples of three-dimensional shapes are cubes, rectangular solids, prisms, cylinders, spheres, cones and pyramids. We will look at the volume formulas and surface area formulas of the solids. We will also discuss some nets of solids.
The following figures show some examples of shapes in solid geometry. Scroll down the page for more examples, explanations and worksheets for each shape.
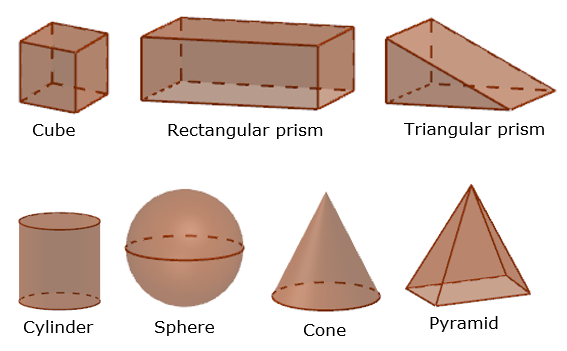
Geometry Worksheets
Practice your skills with the following worksheets:
Printable & Online Geometry Worksheets
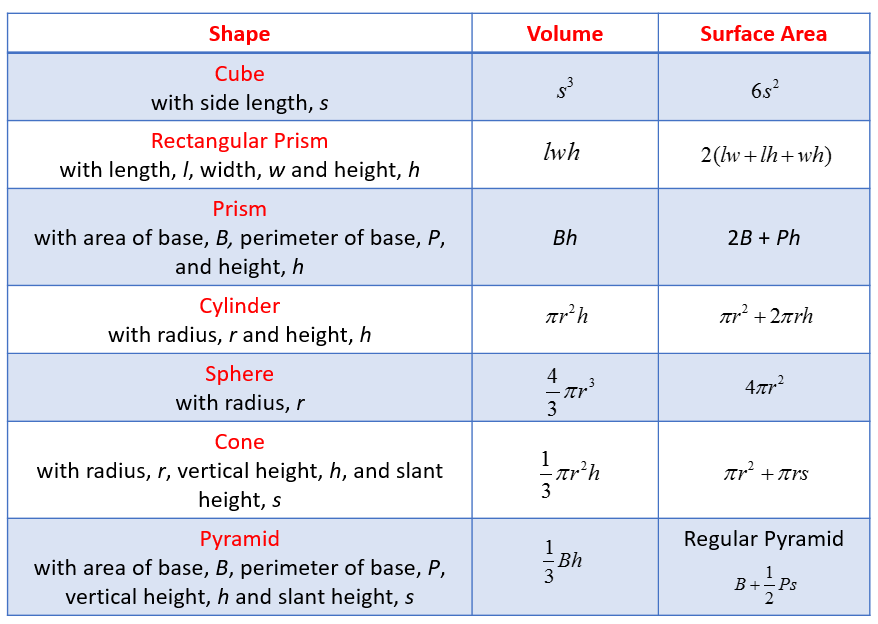
The following table gives the volume formulas and surface area formulas for the following solid shapes: Cube, Rectangular Prism, Prism, Cylinder, Sphere, Cone, and Pyramid.
Cubes
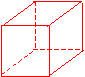
A cube is a three-dimensional figure with six equal square faces.
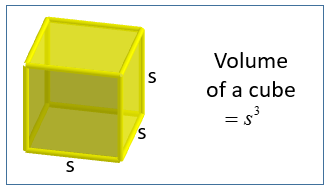
The figure above shows a cube. The dotted lines indicate edges hidden from your view.
If s is the length of one of its sides, then the volume of the cube is s × s × s
Volume of the cube = s3
The area of each side of a cube is s2. Since a cube has six square-shape sides, its total surface area is 6 times s2.
Surface area of a cube = 6s2
Worksheets and more examples
Worksheets on volume and surface area of cubes
More examples on the volume of cubes
More examples on the surface area of cubes
Rectangular Prisms or Cuboids
A rectangular prism is also called a rectangular solid or a cuboid. In a rectangular prism, the length, width and height may be of different lengths.
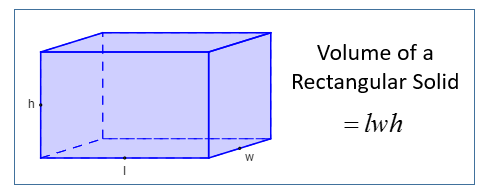
The volume of the above rectangular prism would be the product of the length, width and height that is
Volume of rectangular prism = lwh
Total area of top and bottom surfaces is lw + lw = 2lw
Total area of front and back surfaces is lh + lh = 2lh
Total area of the two side surfaces is wh + wh = 2wh
Surface area of rectangular prism = 2lw + 2lh + 2wh = 2(lw + lh + wh)
Worksheets and more examples
Worksheets on volume and surface area of rectangular prisms
More examples on the volume of rectangular prisms
More examples on the surface area of rectangular prisms
Prisms
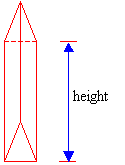
A prism is a solid that has two congruent parallel bases that are polygons. The polygons form the bases of the prism and the length of the edge joining the two bases is called the height.
 |
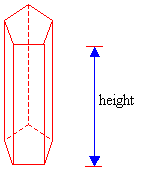 |
| Triangle-shaped base | Pentagon-shaped base |
The above diagrams show two prisms: one with a triangle-shaped base called a triangular prism and another with a pentagon-shaped base called a pentagonal prism.
A rectangular solid is a prism with a rectangle-shaped base and can be called a rectangular prism.
The volume of a prism is given by the product of the area of its base and its height.
Volume of prism = area of base × height
The surface area of a prism is equal to 2 times area of base plus perimeter of base times height.
Surface area of prism = 2 × area of base + perimeter of base × height
Worksheets and more examples
Worksheets on volume of prisms and pyramids
More examples on the volume of prisms
More examples on the surface area of prisms
Cylinders
A cylinder is a solid with two congruent circles joined by a curved surface.
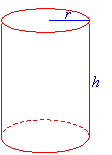
In the above figure, the radius of the circular base is r and the height is h. The volume of the cylinder is the area of the base × height.
Volume of cylinder = πr2h
The net of a solid cylinder consists of 2 circles and one rectangle. The curved surface opens up to form a rectangle.
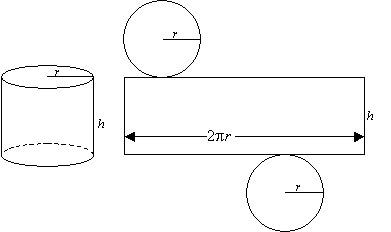
Surface area = 2 × area of circle + area of rectangle
Surface area of cylinder = 2πr2 + 2πrh = 2πr (r + h)
Worksheets and more examples
Worksheets on volume of cylinders
Worksheets on surface area of cylinders
Worksheets on volume and surface area of cylinders
Worksheets on the surface area of cylinders and pipes
More examples on the volume of cylinders
More examples on the surface area of cylinders
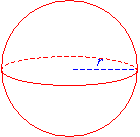
Spheres
A sphere is a solid with all its points the same distance from the center.

Worksheets and more examples
Worksheets on volume of spheres
Worksheets on surface area of spheres
More examples on the volume of spheres
More examples on the surface area of spheres
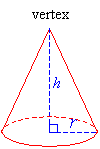
Cones
A circular cone has a circular base, which is connected by a curved surface to its vertex. A cone is called a right circular cone, if the line from the vertex of the cone to the center of its base is perpendicular to the base.
![]()
The net of a solid cone consists of a small circle and a sector of a larger circle. The arc of the sector has the same length as the circumference of the smaller circle.
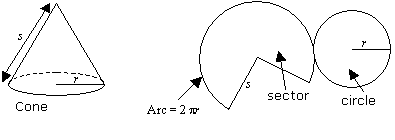
Surface area of cone = Area of sector + area of circle
= πrs + πr2 = πr(r + s)
Worksheets and more examples
Worksheets on the volume of cones
More examples on the volume of cones
More examples on the surface area of cones
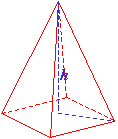
Pyramids
A pyramid is a solid with a polygon base and connected by triangular faces to its vertex. A pyramid is a regular pyramid if its base is a regular polygon and the triangular faces are all congruent isosceles triangles.
![]()
Worksheets and more examples
Worksheets on volume of square pyramids
Worksheets on volume of prisms and pyramids
More examples on the volume of pyramids
More examples on the surface area of pyramids
Worksheets on the surface areas of different solids and composite solids
Worksheet 1 | Worksheet 2 | Worksheet 3 | Worksheet 4 | Worksheet 5
Nets Of A Solid
An area of study closely related to solid geometry is nets of a solid. Imagine making cuts along some edges of a solid and opening it up to form a plane figure. The plane figure is called the net of the solid.
The following figures show the two possible nets for the cube.
 |
 |
 |
How to calculate the volume of prisms, cylinders, pyramids and cones?
Volumes of Prisms and Cylinders = Area of Base × Height
Volumes of Pyramids and Cones = 1/3 × Area of Base × Height
Examples to show how to calculate the volumes of prisms, cylinders, pyramids and cones.
How to calculate the surface area of a pentagonal prism with the base edge of 6 and height of 8?
How to calculate the surface area of cylinders, pyramids and cones?
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.