Surface Area of a Cube
Related Pages
Surface Area Formula
Surface Area of Prisms
Surface Area of a Sphere
More Geometry Lessons
In these lessons, we will learn
- how to calculate the surface area of a cube.
- how to find the length of a cube given the surface area.
- how to use the net of a cube to find its surface area.
- how to find the surface area of a cube in terms of its volume.
Surface Area of a Cube
A cube is a three-dimensional figure with six equal square faces.
The surface area of a cube is the total area of all its faces.
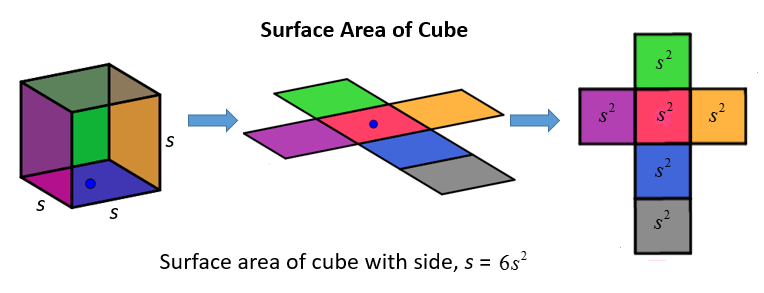
The following figure shows the formula for the surface area of a cube. Scroll down the page for more examples and solutions of finding the surface area of a cube.
Geometry Worksheets
Practice your skills with the following worksheets:
Printable & Online Geometry Worksheets
Worksheet to calculate volume and surface area of cubes
Formula for the Surface Area of a Cube
The formula for the total surface area (SA) of a cube is:
SA = 6s2
Where: SA = Total surface area of the cube s = the length of one side (or edge) of the cube
Explanation and Derivation of the Formula
- A Cube’s Faces: A cube has 6 faces.
- Shape of Each Face: Each face of a cube is a perfect square.
- Area of One Face: The area of a single square face is calculated by multiplying its side length by itself, which is s × s = s2.
- Total Area: Since all 6 faces are identical squares, you multiply the area of one face by 6.
Surface area of a cube (SA) = 6s2.
How to Calculate the Surface Area of a Cube
Example:
Find the surface area of a cube with a side of length 3 cm
Solution:
Given that s = 3
Surface area of a cube = 6s2 = 6(3)2 = 54 cm2
How to find the surface area of a cube?
Example:
Given a side of 3 cm, find the surface area of the cube.
How to find the surface area of a cube?
Step 1: Find the length of a side
Step 2: Substitute into the formula: side × side × 6 and evaluate
Step 3: Write the units
How to find the length of a cube given the surface area?
This video shows how to find the length of a cube given the surface area.
Example: The total surface area of a cube is 216 in2. What is the length of each side of the cube?
How to use the net of a cube to find its surface area?
Another way to look at the surface area of a cube is to consider a net of the cube. The net
is a 2-dimensional figure that can be folded to form a 3-dimensional object.
Imagine making cuts along some edges of a cube and opening it up to form a plane figure. The plane figure is called the net of the cube.
The following net can be folded along the dotted lines to form a cube.
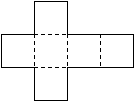
We can then calculate the area of each square in the net and then multiply the area by 6 to get the surface area of the cube.
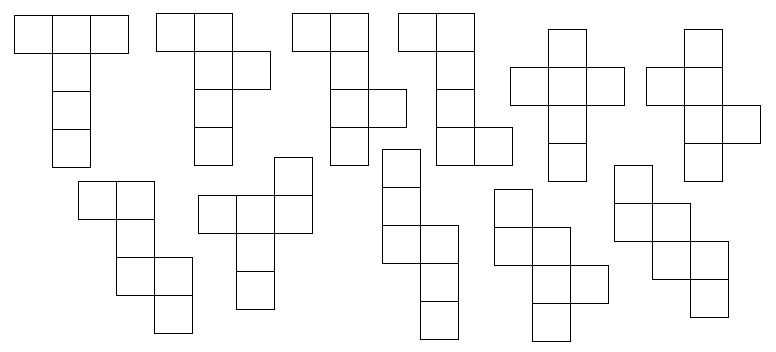
There are altogether 11 possible nets for a cube as shown in the following figures. Notice that the surface area of each of the net is the same.
How to use nets and 3-dimensional figures to find surface area of cubes and prisms?
Surface Area of a Cube in terms of its Volume
How to find the surface area of a cube in terms of volume
S = 6V2/3
Check out our most popular games!
Fraction Concoction Game:
Master fractions in the lab: mix, add, and subtract beakers to create the perfect concoction!
Fact Family Game:
Complete fact families and master the link between addition & subtraction and multiplication & division.
Number Bond Garden:
Clear the board by matching number pairs that sum to ten in this garden-themed mental math puzzle.
Online Addition Subtraction Game:
Practice your addition and subtraction skills to help the penguin find its mummy.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.