Volume Of Sphere

Spheres

Volume of a Sphere
A sphere is a solid with all its points the same distance from the center. The distance is known as the radius of the sphere. The maximum straight distance through the center of a sphere is known as the diameter of the sphere. The diameter is twice the radius.

The volume of a sphere is the amount of three-dimensional space it occupies.

The following figure gives the formula for the volume of a sphere. Scroll down the page for examples and solutions.

Geometry Worksheets
Practice your skills with the following worksheets:
Printable & Online Geometry Worksheets

Formula for the Volume of a Sphere
The volume of a sphere is equal to four-thirds of the product of pi and the cube of the radius.
The formula for the volume (V) of a sphere is:
\(V = \frac{4}{3} πr^3 \)

Where:
V = Volume of the sphere
π (pi) is a mathematical constant, approximately 3.14159.
r = radius of the sphere (the distance from the center of the sphere to any point on its surface)

The formula for the surface area of sphere is:
A = 4πr²

How to calculate the volume of a sphere?

1. Identify the radius (r):
   If you’re given the diameter (d), remember that the radius is half of the diameter: r = d/2.
   If you’re given the surface area (SA), you can find the radius using SA = 4πr², so
   \( r = \sqrt{\frac{SA}{4π}} \)
   
2. Cube the radius (r³) and multiply by 3/4 and π.
   
3. The volume will always be in cubic units.
   

Example:
Calculate the volume of sphere with radius 4 cm.

Solution:
Volume of sphere

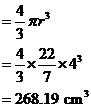
We can also change the subject of the formula to obtain the radius given the volume.

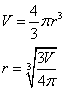
Example:
The volume of a spherical ball is 5,000 cm³. What is the radius of the ball?

Solution:

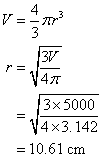
How to use the formula to calculate the volume of a sphere?

Example:
Find the volume of a sphere with a diameter of 14 cm.

• Show Video Lesson

Volume of a hemisphere

What is a hemisphere?

A hemisphere is half a sphere, with one flat circular face and one bowl-shaped face.

How to find the volume of a hemisphere?

The volume of a hemisphere is equal to two-thirds of the product of pi and the cube of the radius.

The volume of a hemisphere is given by the formula:

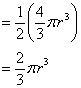
where r is the radius.

How to find the volume of a hemisphere?

Example:
Find the volume of a fishbowl with a diameter of 33cm.

• Show Video Lesson

How to solve word problems about spheres?
The following video shows how to solve problems involving the formulas for the surface area and volume of spheres.

Example:
A sphere has a volume of 288π. Find its area. Leave you answer in terms of π

• Show Video Lesson

Example:
A ball has a diameter of 18 cm.
a) Sketch a cylinder that fits the ball and label its height and base.
b) What is the volume of the cylinder?
c) What is the volume of the ball?

• Show Video Lesson

Example:
The cylinder is melted down into a sphere of radius r. Find an expression for r in terms of x.

• Show Video Lesson

How to proof the Formula of the Volume of a Sphere?
This video gives a proof for the formula of the volume of a sphere that does not involve calculus. This is an "approximated" proof. You would need to use calculus for a more rigorous proof.

• Show Video Lesson

How to derive the formula of a sphere using calculus?

• Show Video Lesson

How Archimedes derived the volume of a sphere?
To do so, he had to use a formula for the volume of a cone.

• Show Video Lesson

Check out our most popular games!
Fraction Concoction	Fact Family Game	Number Bond Garden
Online Addition Subtraction Game	Penguin Solitaire	Sawayama Solitaire
Ark Solitaire	Eldritch Invasion	Shenzhen Solitaire

Check out more Solitaire games here.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.