Volume of Prisms
Solid geometry is concerned with three-dimensional shapes. In these lessons, we will learn
- what is a prism?
- how to find the volume of prisms.
- how to solve word problems about prisms.
Related Pages
Volume Formula
Volume Of Prism Worksheet
Volume Formulas Explained
More Geometry Lessons
Prisms
A prism is a solid that has two parallel faces which are congruent polygons at both ends. These faces form the bases of the prism. A prism is named after the shape of its base.
The other faces are in the shape of parallelograms. They are called lateral faces.
The following diagrams show a triangular prism and a rectangular prism. 
A right prism is a prism that has its bases perpendicular to its lateral surfaces. If the bases are not perpendicular to its lateral bases then it is called an oblique prism.
When we cut a prism parallel to the base, we get a cross section of a prism. The cross section has the same size and shape as the base.
Example:
What is a prism and distinguishes between a right prism and an oblique prism?
How to label the parts of a prism and how to distinguish between an oblique and a right prism?
Volume of a Prism
The volume of a right prism is given by the formula:
Volume = Area of base × height = Ah
where A is the area of the base and h is the height or length of the prism.
Worksheet to calculate volume of prisms and pyramids.
Example:
Find the volume of the following right prism.
Solution:
Volume = Ah
= 25 cm2 × 9 cm
= 225 cm3
Example:
Find the volume of the following right prism
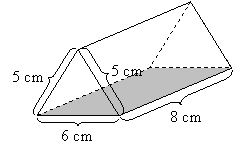
Solution:
First, we need to calculate the area of the triangular base.
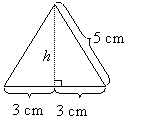
We would need to use Pythagorean theorem to calculate the height of the triangle.
h2 + 32 = 52
Area of triangle = 
= 
× 6 × 4
= 12 cm2
Volume of prism = Ah
= 12 cm2× 8 cm
= 96 cm3
How to find the volume of a rectangular and a triangular prism?
Step 1: Find the area of the base.
Step 2: Multiply the area of the base times the height.
How to find the volume of any prism, right or oblique using a general formula?
Word problems about volume of prisms
The following video shows how to solve a word problem involving the volume of prisms.
Example:
Find the volume and capacity of a swimming pool which is made up of a rectangular and trapezoidal prism.
Use the given net to determine the surface area and volume of a triangular prism
| Check out our most popular games! | ||
|---|---|---|
 Fraction Concoction |
 Fact Family Game |
 Number Bond Garden |
 Online Addition Subtraction Game |
 Penguin Solitaire |
 Sawayama Solitaire |
 Ark Solitaire |
 Eldritch Invasion |
 Shenzhen Solitaire |
Check out more Solitaire games here.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.