Surface Area Of A Pyramid
Related Pages
Surface Area Formulas
Surface Area of Prisms
Surface Area of a Sphere
More Geometry Lessons
In these lessons, we will learn
- how to find the surface area of any pyramid.
- how to find the surface area of a regular pyramid.
- how to find the surface area of a square pyramid.
- how to find the surface area of a pentagonal and a hexagonal pyramid.
- how to find the surface area of a pyramid when the slant height is not given.
Surface Area Of A Pyramid
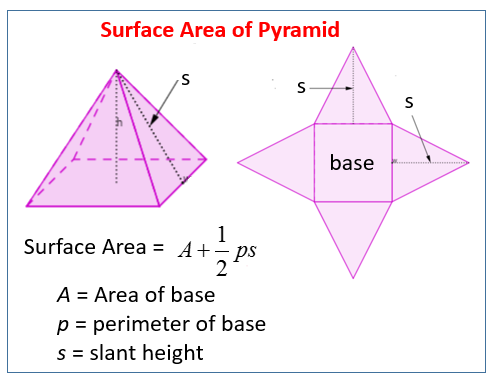
The surface area of a pyramid is the total area of all its faces, including its base and all its triangular lateral faces.
The following diagrams show how to find the surface area of a pyramid. Scroll down the page for more examples and solutions.
Geometry Worksheets
Practice your skills with the following worksheets:
Printable & Online Geometry Worksheets
A pyramid is a solid with a polygonal base and several triangular lateral faces. The lateral faces meet at a common vertex. The number of lateral faces depends on the number of sides of the base. The height of the pyramid is the perpendicular distance from the base to the vertex.
A regular pyramid has a base that is a regular polygon and a vertex that is above the center of the polygon. A pyramid is named after the shape of its base. A rectangular pyramid has a rectangle base. A triangular pyramid has a triangle base.

We can find the surface area of any pyramid by adding up the areas of its lateral faces and its base.
Surface area of any pyramid = area of base + area of each of the lateral faces
If the pyramid is a regular pyramid, we can use the formula for the surface area of a regular pyramid.
Surface area of regular pyramid = area of base + 1/2 ps
where p is the perimeter of the base and s is the slant height.
If the pyramid is a square pyramid, we can use the formula for the surface area of a square pyramid.
Surface area of square pyramid = b2 + 2bs
where b is the length of the base and s is the slant height.
Worksheets:
Calculate the volume of square pyramids
Calculate the volume of prisms & pyramids
Example:
Calculate the surface area of the following pyramid.

Solution:
Sketch a net of the above pyramid to visualize the surfaces.

Since the given pyramid is a square pyramid, we can use any of the above formulas.
Using the formula for the surface area of any pyramid:
Area of base = 6 × 6 = 36 cm2
Area of the four triangles = 1/2 × 6 × 12 × 4 = 144 cm2
Total surface area = 36 + 144 = 180 cm2
Using the formula for a regular pyramid
Surface area of regular pyramid = area of base + 1/2 ps
= 6 × 6 + 1/2 × 6 × 4 × 12 = 180 cm2
Using the formula for a square pyramid
Surface area of square pyramid = b2 + 2bs
= 6 × 6 + 2 × 6 × 12 = 180 cm2
Surface Area Of Pyramid By Adding Up The Area Of Each Surface
How to find the surface area of a pyramid by adding up the area of each surface?
Calculate the surface area of the square based pyramid.
Example:
Find the surface area of a square pyramid with s = 40in, h = 39in and n = 44in
Surface Area Of Square Pyramid By Using A Formula
How to find the surface area of a square pyramid using the formula?
Surface area = 2bs + b2 where b is the length of the base
and s is the slant height.
Solve Word Problems With Pyramids
Example:
What is the surface area of a square pyramid with a base area of 255 square inches and a height of 7 inches?
The Great Pyramid of Khufu, the largest of the pyramid in Giza, was built approximately 4,500 years ago. Today, the height of the pyramid is about 455 feet, which is about 30 feet shorter than it was originally. If you were to walk completely around the base of the pyramid, you would have gone about 3,024 feet.
What is the lateral surface area of the great pyramid today?
Surface Area Of Regular Pyramid By Using A Formula
These videos show how to calculate the surface area of a regular pyramid using the formula:
surface area = area of base + 1/2 × perimeter of base × slant height.
S = B + 1/2 p l
Surface Area Of Pentagonal And Hexagonal Pyramids
This video provides a specific example of how to find the surface area of a pyramid, given base edge and height. The base is a pentagon. It shows how to find the apothem and slant height.
How To Find The Surface Area Of A Pentagonal Pyramid With The Known Apothem?
Surface Area Of Regular Pyramid When The Slant Height Is Not Given
How to calculate the surface area of a square pyramid when the slant height is not given?
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.