Surface Area Of Prisms
In these lessons, we will learn how to:
- calculate the surface area of prisms: rectangular prisms, triangular prisms, trapezoidal prisms, hexagonal prisms etc.
- solve problems about prisms.
- calculate the surface area of prisms using nets.
Related Pages
Surface Area Formulas
Surface Area of Cuboids
Surface Area of a Sphere
More Geometry Lessons
What Is A Prism?
A prism is a solid that has two parallel faces which are congruent polygons at both ends. These faces form the bases of the prism. A prism is named after the shape of its base. The other faces are in the shape of parallelograms. They are called lateral faces.
The following diagrams show a triangular prism and a rectangular prism.
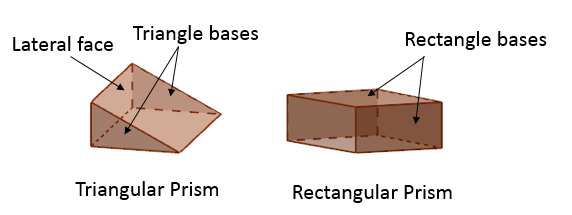
A right prism is a prism that has its bases perpendicular to its lateral surfaces.
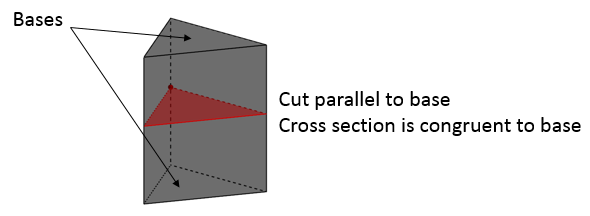
When we cut a prism parallel to the base, we get a cross section of a prism. The cross section is congruent (same size and shape) as the base, as can be seen in the following diagram.
How To Calculate The Surface Area Of A Prism?
The surface area of a prism is the
total area of all its external faces.
Step 1: Determine the shape of each face.
Step 2: Calculate the area of each face.
Step 3: Add up all the areas to get the total surface area.
We can also use the formula:
Surface area of prism = 2 ×
area of base + perimeter of base × height
Worksheet to calculate the surface area and volume of a rectangular prism
Example:
Calculate the surface area of the following prism.
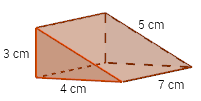
Solution:
There are 2 triangles with the base = 4 cm and height = 3 cm.
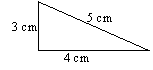
Area of the 2 bases:
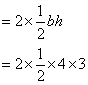
= 12 cm2
1 rectangle with length = 7 cm and width = 5 cm
Area = lw = 7 × 5 = 35 cm2<
1 rectangle with length = 7 cm and width 3 m
Area = lw = 7 × 3 = 21 cm2
1 rectangle with length = 7 cm and width 4 m
Area = lw = 7 × 4 = 28 cm2
The total surface area is 12 + 35 + 21 + 28 = 96 cm2
We can also use the formula:
Surface area of prism = 2 × area of base + perimeter of base × height
= 2 × 6 + (3 + 4 + 5) × 7 = 96 cm2
Example:
The diagram shows a prism whose base is a trapezoid. The surface
area of the trapezoidal prism is 72 cm2. Find the value of x.
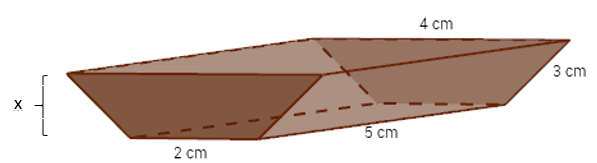
Solution:
There are 2 rectangles with length = 5 cm and width = 3 cm
Area = 2 × 5 × 3 = 30 cm2
There is one rectangle with length = 5 cm and width = 4 cm
Area = 5 × 4 = 20 cm2
There is one rectangle with length = 5 cm and width = 2 cm
Area = 5 × 2 = 10 cm2
There are two trapezoids.
Area = 
cm2 = 6x cm2
Sum of area
30 + 20 + 10 + 6x = 72
60 + 6x = 72
x = 2
The value of x is 2.
How To Find The Surface Area Of Different Types Of Prisms
This video shows how to find the surface area of prisms: cuboid
(or rectangular prism), triangular prism, trapezoidal prism.
How To Find The Surface Area Of A Rectangular Prism?
How To Find The Surface Area Of A Triangular Prism Using The Formula SA = ab+(s1+s2+s3)h?
How To Find The Surface Area Of A Pentagonal Prism?
How To Find The Surface Area Of A Hexagonal Prism?
How To Find The Surface Area Of A Octagonal Prism?
Word Problems About Prisms
How to find the surface area of prisms and cylinders using a given formula? How to solve word problems and composite figures?
Problem: A treasure chest is a composite figure. If you were to paint the surface area, how many square feet would you paint? Round your answer to the nearest square feet.
Surface Area Of Prisms Using Nets
This video shows how to find the surface area of a cube, rectangular prism and triangular prism using nets.
How To Find The Surface Area Of A Hexagonal Prism Using A Net?
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.