Area Of A Sector And Segment

The following table gives the formulas for the area of sector and area of segment for angles in degrees or radians. Scroll down the page for more explanations, examples and worksheets for the area of sectors and segments.

• Printable & Online Circle Worksheets

  Printable
  Circumference Worksheets
  Area of Circle Worksheets
  Area & Circumference Worksheets
  Find Radius from Circumference
  Find Radius from Area
  Find Area from Circumference or vice versa
  Circle Word Problems
  

  Online
  Circumference of Circle
  Area of Circle
  Area & Circumference of Circle
  
  Circle Problems: Circumference, Area
  Circle Word Problems 1
  Circle Word Problems 2
  
  Area of shaded regions that include circles
  Area of figures that include circles
  Area of figures that include circles
  
  Arc Length & Area of Sector (Degrees)
  Arc Length & Area of Sector (Radians)
  Convert between Radians and Degrees

Area Of Sector

A sector is like a “pizza slice” of the circle. It consists of a region bounded by two radii and an arc lying between the radii.

The area of a sector is a fraction of the area of the circle. This area is proportional to the central angle. In other words, the bigger the central angle, the larger is the area of the sector.

The following diagrams give the formulas for the area of circle and the area of sector. Scroll down the page for more examples and solutions.

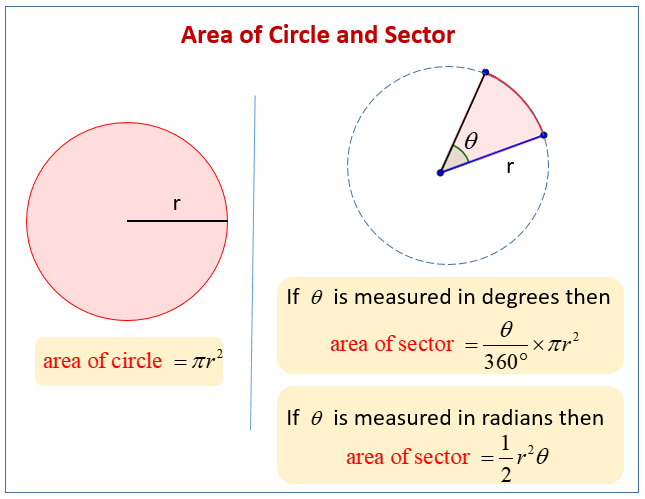
Formula For Area Of Sector (In Degrees)

We will now look at the formula for the area of a sector where the central angle is measured in degrees.

Recall that the angle of a full circle is 360˚ and that the formula for the area of a circle is πr².

Comparing the area of sector and area of circle, we derive the formula for the area of sector when the central angle is given in degrees.

where r is the radius of the circle.

This formula allows us to calculate any one of the values given the other two values.

Worksheet to calculate arc length and area of a sector (degrees)

Calculate The Area Of A Sector (Using Formula In Degrees)

We can calculate the area of the sector, given the central angle and radius of circle.

Example:
Given that the radius of the circle is 5 cm, calculate the area of the shaded sector. (Take π = 3.142).

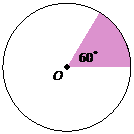
Solution:

Area of sector = 60°/360° × 25π
    = 13.09 cm²

Calculate Central Angle Of A Sector

We can calculate the central angle subtended by a sector, given the area of the sector and area of circle.

Example:
The area of a sector with a radius of 6 cm is 35.4 cm². Calculate the angle of the sector. (Take π = 3.142).

Solution:

Central Angle = 35.4/36π × 360°
    = 112.67°

How To Derive The Formula To Calculate The Area Of A Sector In A Circle?

It explains how to find the area of a sector of a circle. The formula for the area of a circle is given and the formula for the area of a sector of a circle is derived.

Example:
Janice needs to find the area of the red section of the circular table top in order to buy the right amount of paint. What is the area of the red section of the circular table top?

Solution:
Step 1: Find the area of the entire circle using the area formula A = πr².
Step 2: Find the fraction of the circle by putting the angle measurement of the sector over 360°, the total number of degrees in a circle.
Step 3: Multiply the fraction by the area of the circle. Leave your answer in terms of π.

• Show Video Lesson

How To Calculate The Area Of A Sector Using The Formula In Degrees And The Missing Radius Given The Sector Area And The Size Of The Central Angle?

Example 1: Find the area of the shaded region.

Example 2: Find the radius of the circle if the area of the shaded region is 50π

• Show Video Lesson

Formula For Area Of Sector (In Radians)

Next, we will look at the formula for the area of a sector where the central angle is measured in radians. Recall that the angle of a full circle in radians is 2π.

Comparing the area of sector and area of circle, we get the formula for the area of sector when the central angle is given in radians.

where r is the radius of the circle.

This formula allows us to calculate any one of the values given the other two values.

Worksheet to calculate arc length and area of sector (radians)

Calculate The Area Of Sector (Using Formula In Radians)

The following video shows how we can calculate the area of a sector using the formula in radians.

Example:
A lawn sprinkler located at the corner of a yard rotates through 90° and sprays water 30ft. What is the area of the sector watered?

• Show Video Lesson

How To Determine The Area Of A Sector?

The formula is given in radians.
How to determine the area of a segment? (the area bounded by a chord and an arc).

Example 1: Find the area of the sector of a circle with radius 8 feet formed by a central angle of 110°

Example 2: Find the area of the shaded region in the circle with radius 12cm and a central angle of 80°.

• Show Video Lesson

Area Of Segment (Angle In Degrees)

The segment of a circle is a region bounded by the arc of the circle and a chord.

The area of segment in a circle is equal to the area of sector minus the area of the triangle.

How To Derive The Area Of A Segment Formula?

How do you find the area of a segment of a circle?

• Show Video Lesson

How To Calculate The Area Of Segments Of Circles?

It uses half the product of the base and the height to calculate the area of the triangle.

• Show Video Lesson

How To Calculate The Area Of Sector And The Area Of Segment?

It uses the sine rule to calculate the area of triangle.

• Show Video Lesson

Area Of Segment (Angle In Radians)

Finding the area of a segment (angle given in radians)

• Show Video Lesson

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.