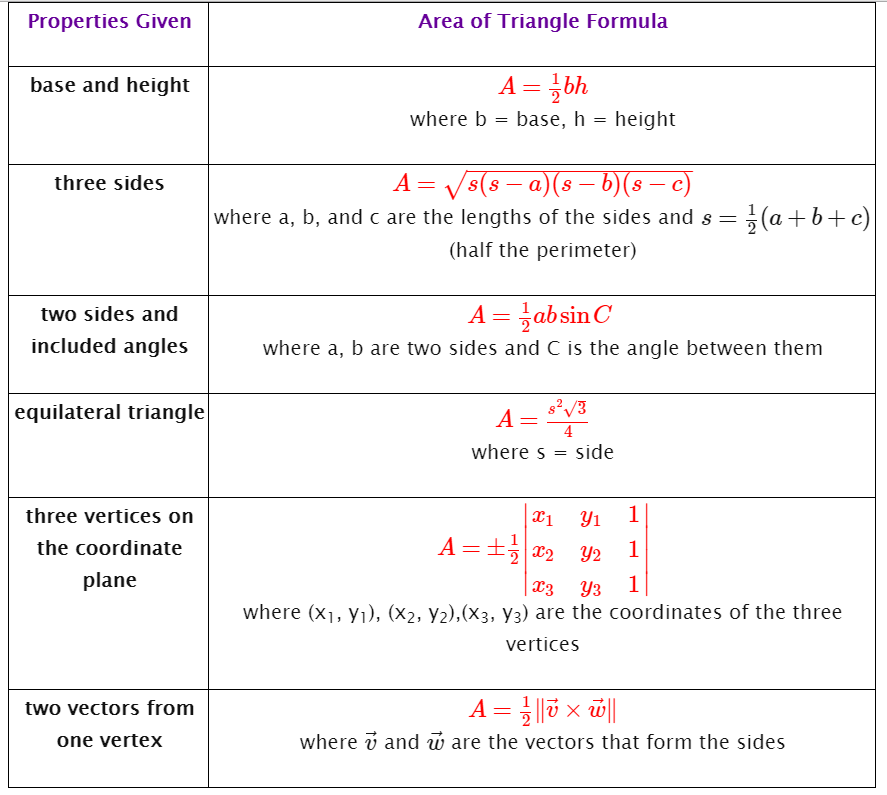
Area Of Triangles - Formulas
Related Pages
Types Of Triangles
Word Problems - Area of Triangles
More Geometry Lessons
In these lessons, we will look at different formulas that can be used to calculate the area of triangles when we are given
- Base and Height
- the Length of Three Sides (Heron’s formula)
- Side, Angle, Side
- an Equilateral Triangle
- a Triangle drawn on a Grid
- Three Vertices on the Coordinate Plane
- Two Vectors from One Vertex
Area Of Triangles
The following table gives the formulas for the area of triangles given some properties about the triangles. Scroll down the page if you need more explanations about the formulas, how to use them as well as worksheets.
Given Base And Height
If we are given the base of the triangle and the perpendicular height then we can use the formula.
\(A = \frac{1}{2}bh\)
Area of a triangle is equal to half of the product of its base and height.
The height of a triangle is the perpendicular distance from a vertex to the base of the triangle.
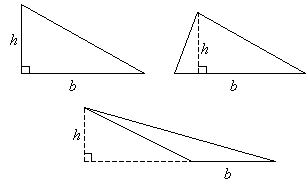
Any of the 3 sides of a triangle can be used as a base. It all depends on where the height is drawn.
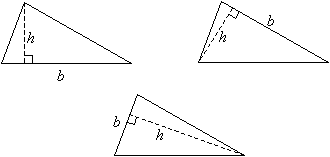
If you are given the sides of an isosceles or equilateral triangle, you can use the Pythagorean Theorem to find the height of the triangle and then use the above formula to find the area.
How to calculate the area of a triangle when given the base and height?
How to use the Pythagorean theorem to get the height of an isosceles triangle and then calculate the area of the triangle?
Worksheets
Worksheet to calculate the areas of triangles
Finding areas of triangles and parallelograms
Finding the height given the area of the triangle
Problems involving the base, height and area of a triangle
Given Length Of Three Sides
If we are given three sides of a triangle, we can use Heron’s formula:
where a, b, and c are the lengths of the sides and s is half the perimeter.
Use Heron’s Formula to determine the area of a triangle while only knowing the lengths of the sides
Given Side Angle Side
If we are given the lengths of two sides of a triangle and the size of angle between them we can use the
formula:
\(Area = \frac{1}{2}ab\sin C\)
The area of a triangle is equal to half the product of two sides times the sine of the included angle. This is also known as the sine rule for the area of a triangle.
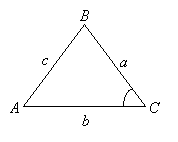
By considering sin A and sin B in a similar way, we obtain
\(Area = \frac{1}{2}bc\sin A\) or \(Area = \frac{1}{2}ac\sin B\)
We may use any of the above formulas depending on which two sides and angle are given.
Remember that the given angle must be between the two given sides.
Example:
Find the area of triangle PQR if p = 6.5 cm, r = 4.3 cm and Q = 39˚. Give your answer
correct to 2 decimal places.
Solution:
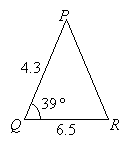
Area of triangle PQR
= 1/2 pr sin Q
= 1/2 × 6.5 × 4.3 × sin 39˚ = 8.79 cm2
How to find the area of an oblique triangle when given two sides and an angle?
Given Equilateral Triangle
To find the area of an equilateral triangle, we can use the Pythagorean Theorem
to get the height of the triangle and then use formula
\(A = \frac{1}{2}bh\)
or we can use the following formula:
The formula for the area of an equilateral triangle (with all sides congruent) is equal to
\(A = \frac{{{s^2}\sqrt 3 }}{4}\)
where s is the length of any side of the triangle.
How to find the area of an equilateral triangle with side s?
Given A Triangle Drawn On A Grid
If the triangle is drawn on a grid then we can use the "box" method to calculate the area of the triangle.
This method involves drawing a smallest box that will enclose the triangle. Make sure that the box follows the grid of the graph paper. The space between the triangle and box is subdivided into right triangles and rectangles and the total area of the space is calculated. The area of the required triangle is then the area of the space subtracted from the area of the box.
How to use the box method to calculate the area of a triangle drawn on a grid?
Given Three Vertices On The Coordinate Plane
When we are given three vertices of a triangle on the coordinate plane, we should first check whether the three vertices form a right triangle. If it is a right triangle then we can use the formula of half the product of its base and height to calculate the area.
If it not a right triangle then we can either use Heron’s formula or the determinant of a matrix.
To use Heron’s formula, we need to first get the length of each side by using the distance formula. Then plug the values into the Heron’s formula.
where a, b, and c are the lengths of the sides and s is half the perimeter.
If you are familiar with matrices and determinants, then you can use the determinant of a matrix to get the area of the triangle.
The area of a triangle is equal to
\(\pm \frac{1}{2}\left| {\begin{array}{*{20}{c}}{{x_1}}&{{y_1}}&1\\{{x_2}}&{y{}_2}&1\\{{x_3}}&{{y_3}}&1\end{array}} \right|\)
where (x1, y1), (x2, y2), (x3, y3) are the coordinates of the three vertices.
The plus/minus (±) sign is meant to take whichever sign is needed to make the answer positive. If the answer is zero, then the three points are collinear (forms a straight line).
Using the determinant of a matrix we can find the area of a triangle whose coordinates are on the coordinate plane.
Example:
Black-necked stilts are birds that live throughout Florida and surrounding areas but breed mostly in the
triangular region shown on the map. Estimate the area of this region. The coordinates given are measured
in miles.
How to find the area of a triangle with the determinant of a matrix?
Given Two Vectors From One Vertex
If we are given the three vertices of a triangle in space, we can use cross products to find the area of the triangle.
If a triangle is specified by vectors u and v originating at one vertex, then the area is half
the magnitude of their cross product.
\(A = \frac{1}{2}\left\| {\overrightarrow u } \right. \times \left. {\overrightarrow v } \right\|\)
How to compute the area of a triangle given its three vertices in space, using cross products?
Example:
A triangle in R3 has vertices at points (1, 2, 3), (5, 5, 5) and (7, 8, 9). What is the area?
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.