Geometry - Nets Of Solids

What Is Meant By The Net Of A Solid?

A geometry net is a 2-dimensional shape that can be folded to form a 3-dimensional shape or a solid. Or a net is a pattern made when the surface of a three-dimensional figure is laid out flat showing each face of the figure. A solid may have different nets.

Here are some steps to determine whether a net forms a solid:

1. Make sure that the solid and the net have the same number of faces and that the shapes of the faces of the solid match the shapes of the corresponding faces in the net.
2. Visualize how the net is to be folded to form the solid and make sure that all the sides fit together properly.

Nets are helpful when we need to find the surface area of the solids.

Nets Of Prisms, Pyramids, Cylinders And Cones

Here are some examples of nets of solids: Prism, Pyramid, Cylinder and Cone. Scroll down the page for more examples and solutions.

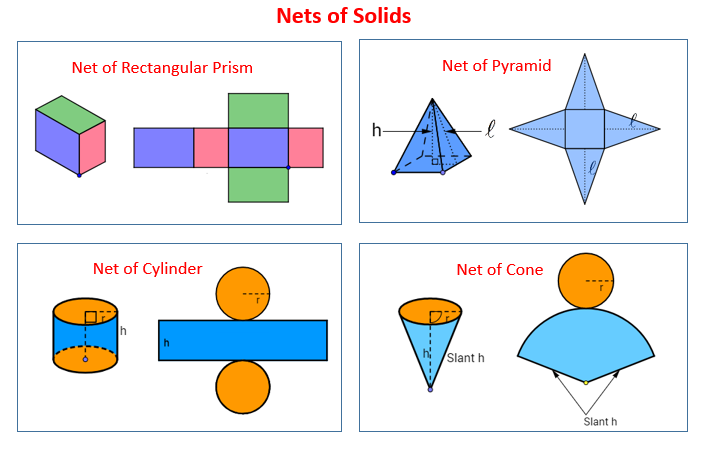
• Nets & Surface Area Worksheets

  Printable
  Nets of Solid Figures
  Find Surface Area using Nets
  Surface Area of Rectangular Prisms
  Surface Area of Right Prisms
  Surface Area of Solids (include composite solids)
  

  Online
  Surface Area of Cylinder
  Surface Area of Sphere
  Surface Area of Solids I
  Surface Area of Solids II
  Surface Area of Solids III
  Surface Area of Solids IV
  Surface Area of Solids V
  Surface Area of Cylinders & Pipes
  Surface Area of Cylinders & Spheres
  

What Is The Net Of A Cube?

A cube is a three-dimensional figure with six equal square faces.

 

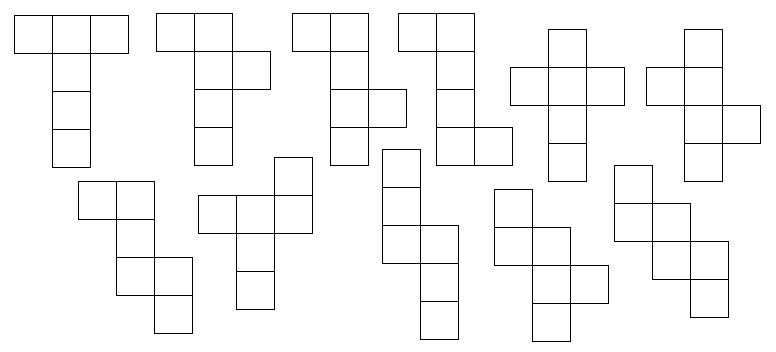
How many nets are there for a cube?

There are altogether 11 possible nets for a cube as shown in the following figures.

What is the net of a rectangular prism or cuboid?

A rectangular prism or cuboid is formed by folding a net as shown:

How to draw a net of a rectangular prism or cuboid?

• Show Video Lesson

How to create different nets of a cube and rectangular prism?

• Show Video Lesson

Nets of prisms and pyramids.
Learn about faces, edges and vertices.

• Show Video Lesson

Analyze the net of a cylinder to determine volume and surface area
The diagram below shows a net for a cylinder.
a. Suppose the net is assembled. Find the volume of the cylinder.
b. Find the surface area of the cylinder.

• Show Video Lesson

How to use nets and 3-dimensional figures to find surface area of cubes and prisms?

• Show Video Lesson

Interactive animations for nets of solids

For animations to explore how 3D shapes unfold into nets and how nets fold to form geometric solids, see: 3D Nets Animations

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.