Equilateral Triangles, Isosceles Triangles and Scalene Triangles
In these lessons, we will learn to
- classify triangles by length of sides: Equilateral Triangles, Isosceles Triangles, Scalene Triangles
- solve some problems involving angles and sides of triangles
Triangles are polygons that have three sides, three vertices and three angles.
One way to classify triangles is by the length of their sides.
How are triangles classified?
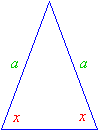
Isosceles Triangles
An isosceles triangle has two sides of equal length. The angles opposite the equal sides are also equal. These two angles are called the base angles.
Example:
An isosceles triangle has one angle of 96º. What are the sizes of the other two angles?
Solution:
Step 1: Since it is an isosceles triangle it will have two equal angles. The given 96º angle cannot be one of the equal pair because a triangle cannot have two obtuse angles.
Step 2: Let x be one of the two equal angles. The sum of all the angles in any triangle is 180°.
x + x + 96° = 180° ⇒ 2x = 84° ⇒ x = 42°
Answer:
The sizes of the other two angles are 42° each.
Equilateral Triangles
An equilateral triangle has all three sides equal in length. Its three angles are also equal and they are each 60º. Therefore, an equilateral triangle is also an equiangular triangle.
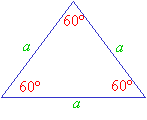
An equilateral triangle can be considered a special case of isosceles triangle, having all three sides equal.
Scalene Triangles
A scalene triangle has no sides of equal length. Its angles are also all different in size.

The shortest side would be opposite the smallest angle. The longest side will be biggest angle.
The following videos shows the different types of triangles and some problems involving the angles.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.