Relative Frequency Histogram Worksheet

Printable “Statistics” Worksheets:
Statistical Questions
Categorical vs. Numerical Data
Create Dot Plots
Interpret Dot Plots
Histograms
Relative Frequency Histograms

Free printable and online worksheets to help Grade 6 students review how to construct and interpret a relative frequency histogram.

Relative Frequency Histogram

A relative frequency histogram is a type of histogram where each bar represents the relative frequency of data points within each bin, rather than the absolute frequency. We can obtain the relative frequency by dividing the number of data points in the bin by the total number of data points in the dataset.

Steps to Create a Relative Frequency Histogram

1. Gather the numerical data you want to visualize.
2. Decide how many intervals (bins) you want to divide your data into. This can be determined based on the range of the data and the level of detail desired. Usually about 5 to 10 bins would be suitable.
3. Calculate the bin width by subtracting the minimum value from the maximum value and then dividing by the number of bins.
4. Calculate Relative Frequencies: For each bin, divide the frequency (count) of data points by the total number of data points to get the relative frequency. Create the frequency distribution by counting how many data points fall into each bin.
5. Draw the Relative Frequency Histogram:
   On the horizontal axis, place the bins (intervals).
   On the vertical axis, place the relative frequencies.
   Draw bars for each bin with heights corresponding to their relative frequencies.

Interpreting Histograms Distributions

 

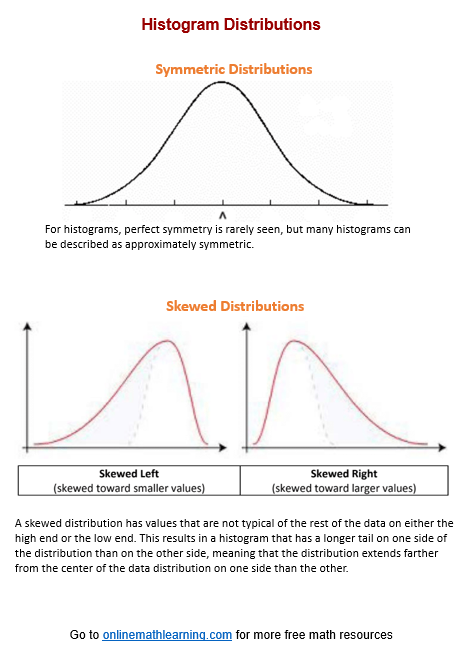
Shape of Distribution:
Symmetrical: The left and right sides are approximately mirror images.
Skewed Left (Negative Skew): The left tail is longer; most data points are on the right.
Skewed Right (Positive Skew): The right tail is longer; most data points are on the left.

Modality:
Unimodal: One peak.
Bimodal: Two peaks.
Multimodal: More than two peaks.

Spread and Range:
Indicates the variability of the data.
Wide spread suggests high variability; narrow spread suggests low variability.

Outliers:
Data points that fall far outside the range of most other points.
Can be identified as isolated bars at either end of the histogram.

Have a look at this video if you need to review how to create and interpret a relative frequency histogram.

• Construct a relative frequency histogram

Click on the following worksheet to get a printable pdf document.
Scroll down the page for more Relative Frequency Histogram Worksheets.

 

More Relative Frequency Histogram Worksheets

Printable
(Answers on the second page.)
Relative Frequency Histogram Worksheet #1
Relative Frequency Histogram Worksheet #2
Relative Frequency Histogram Worksheet #3
Relative Frequency Histogram Worksheet #4

Related Lessons & Worksheets

Relative Frequency Histogram

More Printable Worksheets

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.