Distance Formula
In these lessons, we will learn
- how to derive the distance formula from the Pythagorean Theorem.
- how to use the distance formula.
Related Pages
Pythagoras' Theorem
Midpoint Formula
Coordinate Geometry
Geometry Lessons
Check out the distance formula calculator near the end of this page that can calculate the distance between two points. Use it to check your answers.
The following figures give the Distance Formula and how the Distance Formula is derived from the Pythagorean Theorem. Scroll down the page for more examples and solutions.
In the coordinate plane, we can use the distance formula to find the distance between any two points. The distance formula can be derived from the Pythagorean Theorem.
The distance between the two points (x1,y1) and (x2,y2) is given by the distance formula.
Example:
To find the distance between the points P(2, 3) and Q(1, 1). We can sketch the right-angled triangle
PQR with PQ as the hypotenuse.
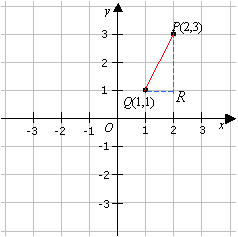
Solution:
Using Pythagorean theorem: PQ2 = (2 – 1)2 + (3 –1)2
⇒ PQ = 
In general, the distance between two points P(x1,y1) and Q(x2,y2) is given by the distance formula:
Example:
Find the distance between the points A(1, 2) and B(-3, -2).
Solution:
Using the distance formula:
Distance =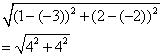 
= 5.66 (correct to 2 decimal places)
Distance Formula Worksheet 1
Distance Formula Worksheet 2
How The Distance Formula Comes From The Pythagorean Theorem?
Example of finding the distance between two points.
The following videos show the Distance Formula and how to find the Distance Between Two Points
Example:
Suppose you drive from point A(3,8) in a straight line to B(13,14); if you stop halfway how far would you be from point B?
The following video gives another example of using the distance formula
Distance Calculator
This distance formula calculator can calculate the distance between two given points on the coordinate plane.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.