Arc Of A Circle
More Geometry Lessons
In these lessons, we will learn
- the arc of a circle
- the central angle
- the arc measure
- the arc length formula when the arc measure is given in degrees
- the arc length formula when the arc measure is given in radians
- how to calculate the arc length using the arc length formula
Arc of a Circle
An arc is any connected part of the circumference of a circle.
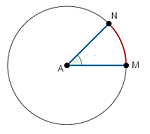
In the diagram above, the part of the circle from M to N forms an arc. It is called arc MN.
An arc could be a minor arc, a semicircle or a major arc.
- A semicircle is an arc that is half a circle.
- A minor arc is an arc that is smaller than a semicircle.
- A major arc is an arc that is larger than a semicircle.
Central Angle
A central angle is an angle whose vertex is at the center of a circle.
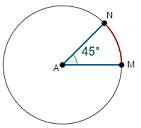
In the diagram above, the central angle for arc MN is 45°.
The sum of the central angles in any circle is 360°.Arc Measure
The measure of a semicircle is 180°.
The measure of a minor arc is equal to the measure of the central angle that intercepts the arc. We can also say that the measure of a minor arc is equal to the measure of the central angle that is subtended by the arc. In the diagram below, the measure of arc MN is 45°.
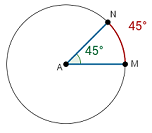
The measure of the major arc is equal to 360° minus the measure of the associated minor arc.
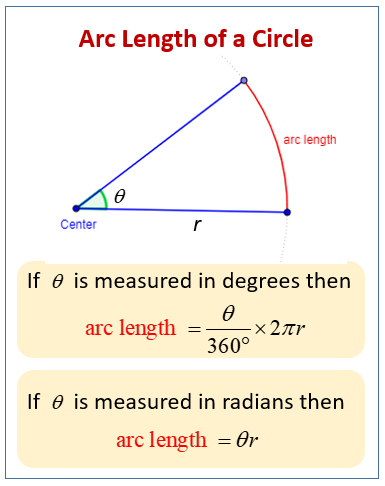
The following video shows how to identify semicircle, minor arc and major arc and their measures.Arc Length Formula
The arc length is the distance along the part of the circumference that makes up the arc.
The following diagram gives the formulas to calculate the arc length of a circle for angle measures in degrees and angle measured in radians. Scroll down the page for more examples and solutions.
Arc Measure given in Degrees
Since the arc length is a fraction of the circumference of the circle, we can calculated it in the following way. Find the circumference of the circle and then multiply by the measure of the arc divided by 360°. Remember that the measure of the arc is equal to the measure of the central angle.
The formula for the arc length of a circle is
where r is the radius of the circle and m is the measure of the arc (or central angle) in degrees.
Worksheet to calculate arc length and area of a sector (degrees).
Arc Measure given in Radians
If the measure of the arc (or central angle) is given in radians, then the formula for the arc length of a circle is the product of the radius and the arc measure.
Arc Length = r × m
where r is the radius of the circle and m is the measure of the arc (or central angle) in radians
The above formulas allow us to calculate any one of the values given the other two values.
Worksheet to calculate arc length and area of sector (radians).Calculate Arc Length given Measure of Arc in degrees
From the formula, we can calculate the length of the arc.
Example:
If the circumference of the following circle is 54 cm, what is the length of the arc ABC?
Solution:
Circumference = 2πr = 54
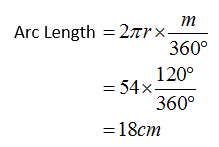
Example:
If the radius of a circle is 5 cm and the measure of the arc is 110˚, what is the length of the arc?
Solution:
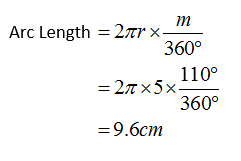
Arc Length in Degrees
These video shows how to define arc length and how it is different from arc measure. They will also show how to calculate the length of an arc when the arc measure is given in degrees.
Arc Length Theorem - How to Find the Length of an Arc?
How to use the Arc Length Formula when the arc measure is given in degrees?
This video lesson discusses how to find the length of an arc. First, the arc length theorem is reviewed and explained. An example of find the length of a major arc is modeled. The given information is the measure of the related minor arc and the radius of the circle. How to find the arc length on a circle when the central angle is given in degrees?
Calculate Arc Length given Measure of Arc in radians
If the measure of the arc (or central angle) is given in radians, then the formula for the arc length of a circle is
Arc Length = r × m
where r is the radius of the circle and m is the measure of the arc (or central angle) in radians
This video shows how to use the Arc Length Formula when the measure of the arc is given in radians. Definition of Arc Length and Finding the Arc Length when the central angle is given in radians.Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.