Angles and Intercepted Arcs
In these lessons, we will learn some formulas relating the angles and the intercepted arcs of circles.
- Measure of a central angle.
- Measure of an inscribed angle: angle with its vertex on the circle
- Measure of an angle with vertex inside a circle.
- Measure of an angle with vertex outside a circle.
We will also learn about angles of Inscribed Triangles and Inscribed Quadrilaterals.
Related Pages
Angles In A Circle
Circles
Conic Sections: Circles
More Geometry Lessons
The following diagrams show the relationships between the Angles and their Arcs: Central Angles, Inscribed Angles, Internal Angles and External Angles. Scroll down the page for more examples, explanations and solutions.
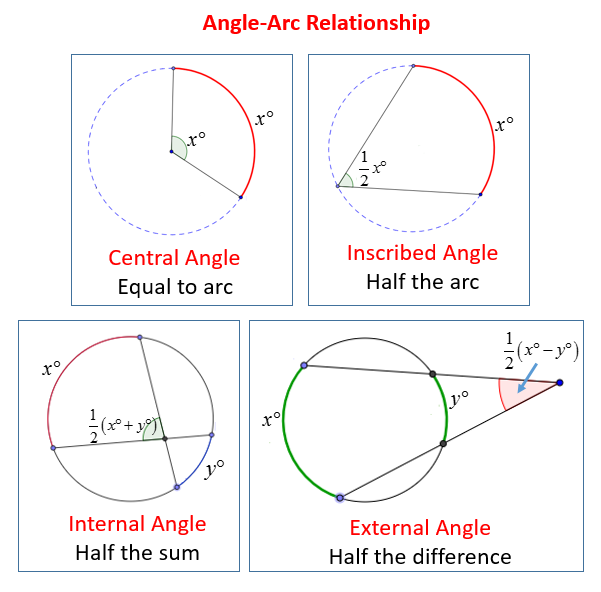
Central Angles And Their Arcs
What is a Central Angle?
A central angle is an angle with its vertex at the center of the circle and its sides are the radii of the circle.
What is the relationship between central angles and their arcs?
The measure of a central angle is equal to the measure of its intercepted arc.
The formula is:
Measure of central angle = measure of intercepted arc
Example:
Find the value of x
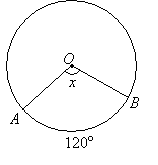
Solution:
x = m∠AOB = minor arc from A to B = 120°
Central Angles and Arcs
A chord is a segment that has its endpoints on a circle.
The diameter is the longest chord of a circle and it passes through the center of a circle.
A line is called a straight angle and it forms a 180 degree angle.
A central angle is an angle with its vertex at the center of a circle and its sides are radii of the same circle.
Show that central angles = arcs they intercept.
Examples to show how to use the property that the measure of a central angle is equal to the measure of its intercepted arc to find the missing measures of arcs and angles in given figures.
Inscribed Angles And Their Arcs
What is an Inscribed Angle?
An inscribed angle is an angle with its vertex on the circle.
What is the relationship between inscribed angles and their arcs?
The measure of an inscribed angle is half the measure the intercepted arc.
The formula is:
Measure of inscribed angle = 1/2 × measure of intercepted arc
Example:
Find the value of x
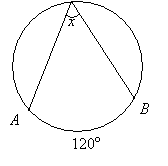
Solution:
x = m∠AOB = 1/2 × 120° = 60°
Angle with vertex on the circle (Inscribed angle)
This video deals with angles formed with vertices on the circle.
Examples of how to use the property that inscribed angles are 1/2 the measure of their intercepted arcs to find missing angles.
Angles With Vertex Inside The Circle And Their Arcs
The measure of an angle with its vertex inside the circle is half the sum of the intercepted arcs.
The formula is
Measure of angle with vertex inside circle = 1/2 × (sum of intercepted arcs)
Example:
Find the value of x
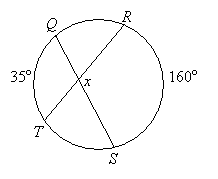
Solution:
1/2 × (160° + 35°) = 97.5°
Angle with vertex inside the circle
The following video shows how to apply the formula for angles with vertex inside the circle to find missing angles.
Angles With Vertex Outside The Circle And Their Arcs
The measure of an angle with its vertex outside the circle is half the difference of the intercepted arcs.
The formula is:
Measure of angle with vertex outside the circle = 1/2 × (difference of intercepted arcs)
Example:
Find the value of x
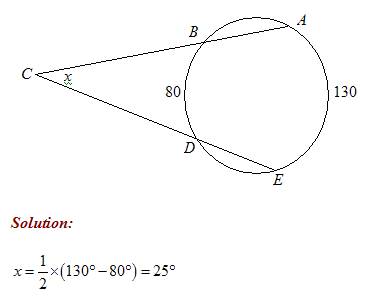
Angle with vertex outside the circle
The following video shows how to apply the formula for angles with vertex outside circle to find missing angles.
Arc And Angle Relationship Problems
This video will go through a few examples of how to use the formulas involving Arc and Angle Relationships to find the measure of missing angles or missing arcs.
More Examples of Arc and Angle Relationship Problems
Inscribed Triangles
If two inscribed angles of a circle intercept the same arc, then the angles are congruent.
An inscribed polygon is a polygon with all its vertices on the circle. The circle is then called a circumscribed circle.
If a right triangle is inscribed in a circle, then the hypotenuse is a diameter of the circle.
Conversely, if one side of an inscribed triangle is a diameter, then the triangle is a right triangle, and the angle opposite the diameter is a right angle.
Right Triangles Inscribed in Circles (Proof)
Proof showing that a triangle inscribed in a circle having a diameter as one side is a right triangle.
Inscribed Quadrilaterals
A quadrilateral is inscribed in a circle if and only if its opposite angles are supplementary.
How to use this property to find missing angles?
Circles - Inscribed Quadrilaterals
When a quadrilateral is inscribed in a circle:
- The interior angles add up to 360°.
- Both pairs of opposite angles are supplementary.
How to find missing angles inside inscribed quadrilaterals?
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.