Angles In A Circle Theorems

In these lessons, we review and summarise the properties of angles that can be formed in a circle and their theorems.

• Inscribed angles subtended by the same arc are equal.
• Central angles subtended by arcs of the same length are equal.
• The central angle of a circle is twice any inscribed angle subtended by the same arc.
• Angle inscribed in semicircle is 90°.
• An angle between a tangent and a chord through the point of contact is equal to the angle in the alternate segment.
• The opposite angles of a cyclic quadrilateral are supplementary
• The exterior angle of a cyclic quadrilateral is equal to the interior opposite angle.
• A radius or diameter that is perpendicular to a chord divides the chord into two equal parts and vice versa.
• A tangent to a circle is perpendicular to the radius drawn to the point of tangency.
• When two segments are drawn tangent to a circle from the same point outside the circle, the segments are equal in length.

The following figures show the Inscribed Angle Theorems and Angles in Circle Theorems. Scroll down the page for more examples and solutions of Inscribed Angle Theorems and Angles in Circle Theorems.

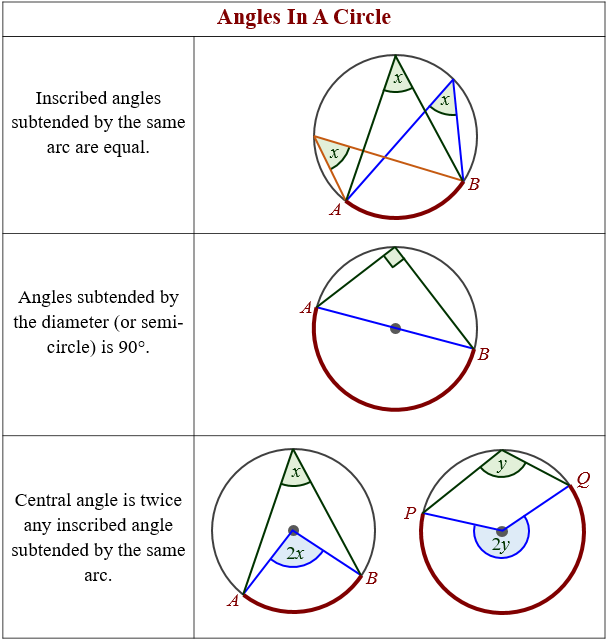
Inscribed Angles Subtended By The Same Arc Are Equal

The following diagram shows inscribed angles subtended by the same arc are equal.

∠x = ∠y because they are subtended by the same arc AEC.

Central Angles Subtended By Arcs Of The Same Length Are Equal

The following diagram shows central angles subtended by arcs of the same length are equal.

∠x = ∠y if arc AB = arc CD

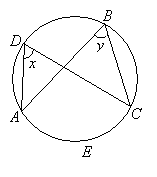
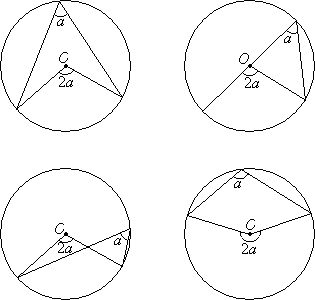
The Central Angle Is Twice The Inscribed Angle

The following diagrams show the central angle of a circle is twice any inscribed angle subtended by the same arc.

Angle Inscribed In Semicircle Is 90°

The following diagram shows the angle inscribed in semicircle is 90 degrees.

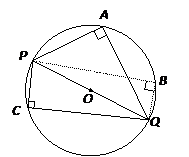
POQ is the diameter. ∠PAQ = ∠PBQ = ∠PCQ = 90˚.

Alternate Segment Theorem

The diagram shows an angle between a tangent and a chord through the point of contact is equal to the angle in the alternate segment.

The alternate segment theorem tells us that ∠CEA = ∠CDE

Angles In A Cyclic Quadrilateral

In a cyclic quadrilateral, the opposite angles are supplementary i.e. they add up to 180°

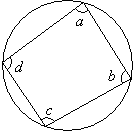
a + c = 180°, b + d = 180°

Exterior Angle Of A Cyclic Quadrilateral Is Equal To The Interior Opposite Angle

The following diagram shows the exterior angle of a cyclic quadrilateral is equal to the interior opposite angle.

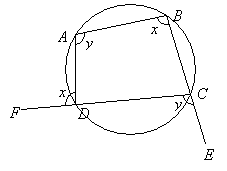
The exterior angle ∠ADF is equal to the corresponding interior angle ∠ABC.

The exterior angle ∠DCE is equal to the corresponding interior angle ∠DAB.

Radius Perpendicular To A Chord Bisects The Chord

A radius or diameter that is perpendicular to a chord divides the chord into two equal parts and vice versa.

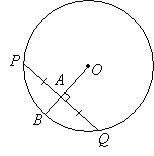
In the above circle, if the radius OB is perpendicular to the chord PQ then PA = AQ.

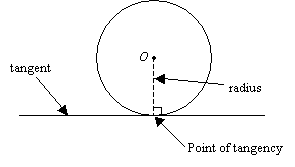
Tangent To A Circle Theorem

A tangent to a circle is perpendicular to the radius drawn to the point of tangency.

Two-Tangent Theorem

When two line segments are drawn tangent to a circle from the same point outside the circle, the segments are equal in length.

In the following diagram:
If AB and AC are two tangents to a circle centred at O, then:

• the tangents to the circle from the external point A are equal.
• OA bisects the ∠BAC between the two tangents.
• OA bisects the ∠BOC between the two radii to the points of contact.
• triangle AOB and triangle AOC are congruent right triangles.

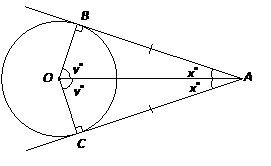
Videos

This video gives a review of the following circle theorems: arrow theorem, bow theorem, cyclic quadrilateral, semi-circle, radius-tangent theorem, alternate segment theorem, chord center theorem, dual tangent theorem.

• Show Video Lesson

This video gives a review of the following circle theorems: same segment, subtended by arc, angle in semicircle, tangents equal length, radius tangent, alternate segment, bisect chord, cyclic quadrilateral. It also includes the proofs of the theorem.

• Show Video Lesson

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.