Cyclic Quadrilaterals - Quadrilaterals Inscribed Within Circles

We will learn what a cyclic quadrilateral is and the related angle properties.

• Opposite angles of a cyclic quadrilateral are supplementary.
• Exterior angle of a cyclic quadrilateral is equal to the interior opposite angle.

We will also prove that the opposite angles of a cyclic quadrilaterals are supplementary.

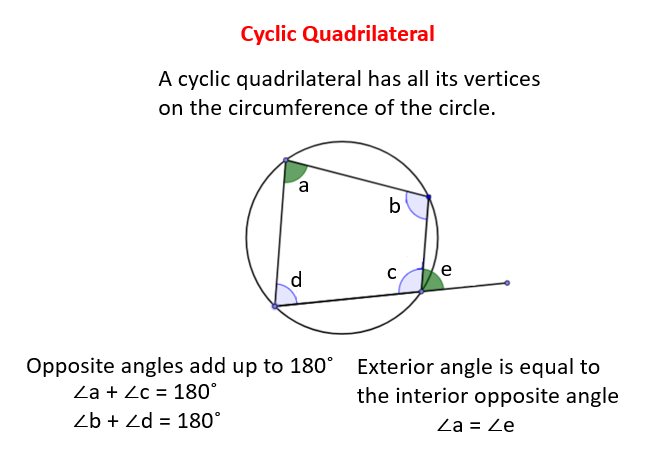
What Is A Cyclic Quadrilateral?

A cyclic quadrilateral is a quadrilateral with its 4 vertices on the circumference of a circle.

The following diagram shows a cyclic quadrilateral and its properties. Scroll down the page for more examples and solutions.

Cyclic quadrilaterals are also called inscribed quadrilaterals or chordal quadrilaterals.

Properties Of A Cyclic Quadrilateral

Property 1: In a cyclic quadrilateral, the opposite angles are supplementary i.e. they add up to 180˚.

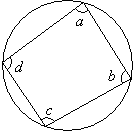
∠a + ∠c = 180˚, ∠b + ∠d = 180˚

Property 2: The exterior angle of a cyclic quadrilateral is equal to the interior opposite angle.

Example:

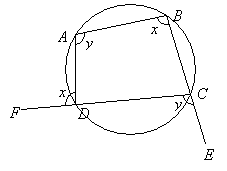
The exterior angle ∠ADF is equal to the corresponding interior angle ∠ABC.

The exterior angle ∠DCE is equal to the corresponding interior angle ∠DAB.

How To Use The Properties Of A Cyclic Quadrilateral To Find Missing Angles?

Example:

AC is a diameter of the circle. Find the value of x.

Solution:
∠ABC = 90˚ (angle of semicircle)
∠ABD + ∠DBC = ∠ABC
∠ABD + 36˚ = 90˚
∠ABD = 54˚
∠ABD + x = 180˚ (interior opposite angles of a cyclic quadrilateral)
x = 180˚ – 54˚ = 126˚

Example:
Find the values of x and y in the following figure.

Solution:
x = 98˚ (Corresponding opposite angles of a cyclic quadrilateral )
y + 27˚ = 53˚ (Corresponding opposite angles of a cyclic quadrilateral)
y = 26˚

Using The Properties Of A Cyclic Quadrilateral To Find Missing Angles

A quadrilateral is cyclic when its four vertices lie on a circle.
Opposite angles in a cyclic quadrilateral adds up to 180˚.

How To Find Missing Angles Using The Properties Of A Cyclic Quadrilateral?

Opposite angles in a cyclic quadrilateral adds up to 180˚.
Interior opposite angles are equal to their corresponding exterior angles.
Find the missing angles using central and inscribed angle properties.
Can you find the relationship between the missing angles in each figure?

• Show Video Lesson

Circle Theorems - Alternate Segment Theorem And Cyclic Quadrilaterals

Exam Practice Question Example:
ABCD is a cyclic quadrilateral within a circle centre O. XY is the tangent to the circle at A.
Angle XAB = 58°, Angle BAD = 78°, Angle DBC = 34°. Prove that AB is parallel to CD.

• Show Video Lesson

Proof That The Opposite Angles Of A Cyclic Quadrilateral Are Supplementary

This video shows how to prove that opposite angles in a cyclic quadrilateral are supplementary.
It is based on the theorem: Angle at the center is twice angle at the circumference.

• Show Video Lesson

Circle Geometry: Cyclic Quadrilateral

What is the relationship between the angles of a quadrilateral that is inscribed in a circle?
This video shows how to prove that opposite angles in a cyclic quadrilateral are supplementary.

• Show Video Lesson

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.