Finding Angles Involving Tangents And Circles
Related Pages
Angles In A Circle
Tangents Of Circles And Angles
Circles
More Geometry Lessons
In this lesson, we will learn about tangents and circles.
We will look at finding angles in diagrams that involve tangents and circles.
Some of the theorems used are:
Tangent to Circle Theorem
Pythagorean Theorem
Two-Tangent Theorem
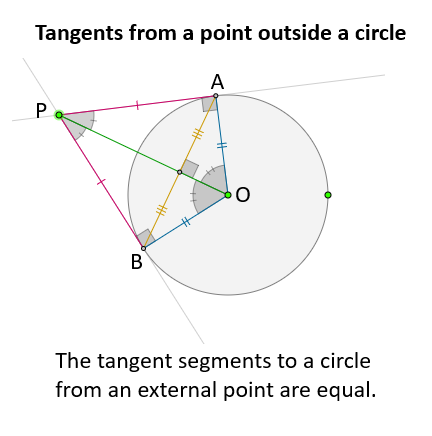
Tangents from a Point Outside a Circle
When a point lies outside a circle, exactly two tangents can be drawn from that point to the circle. These tangents are equal in length and form congruent right triangles with the circle’s radius.
The following diagram shows the properties of the line segments and angles formed by the tangents from a point outside a circle. Scroll down the page for more examples and solutions on how to use the properties to solve for angles.
Geometry Worksheets
Practice your skills with the following Geometry worksheets:
Printable & Online Geometry Worksheets
-
Number of Tangents:
From a point outside a circle, you can draw exactly two tangents to the circle. -
Length of Tangent Segments:
Theorem: The lengths of the tangent segments drawn from an external point to a circle are equal. If point \(P\) is outside a circle with center \(O\), and tangents from \(P\) touch the circle at points \(A\) and \(B\), then \(PA = PB\). -
Angles Subtended at the Center:
The two tangents from an external point subtend equal angles at the center of the circle.
In the scenario above, \(\angle POA = \angle POB\). -
Angle Bisector:
The line segment joining the external point to the center of the circle bisects the angle between the two tangents.
The line segment \(PO\) bisects \(\angle APB\), meaning \(\angle APO = \angle BPO\). -
Right Angles with Radii:
A tangent to a circle is always perpendicular to the radius at the point of tangency.
Therefore, in our example, \(\angle OAP = 90^\circ\) and \(\angle OBP = 90^\circ\). -
Formation of Congruent Triangles:
If you connect the center of the circle to the points of tangency (\(OA\) and \(OB\)) and to the external point \((OP)\), you form two right-angled triangles, \(\triangle OAP\) and \(\triangle OBP\).
These two triangles are congruent by the Right-Hypotenuse-Side (RHS) congruence rule because:
\(\angle OAP = \angle OBP = 90^\circ\) (Right angles)
\(OP\) is common to both triangles (Hypotenuse)
\(OA = OB\) (Radii of the same circle)
The congruence of these triangles is the basis for proving the properties mentioned above (equal tangent lengths and equal angles).
Example:
In the following diagram, PA and PB are tangents to the circle. Find the value of:
a) ∠OAP
b) ∠AOB
c) ∠OBA
d) ∠ASB
e) the length of OP, given PB = 7 cm.

Solution:

How to solve for unknown values using the properties of a tangent line to a circle?
Tangent to Circle Theorem
A line is tangent to a circle if and only if the line is perpendicular to the radius drawn to the point of tangency.
How to solve for unknown values using the properties of tangent segments to a circle from a given point?
Tangent to a Circle from a Point
Tangent segments to a circle from a point are congruent.
Tangent Lines to a Circle
Tangent lines touches the circle at only one point
Point of Tangency is where the tangent line touches the circle.
Example:
Is AB a tangent line?
Find the missing angles.
How to use the Properties of Tangents to find missing angles or sides?
Terms to know
A circle is a set of all points in a plane equidistant from a given point.
A radius is a segment whose endpoints are the center and a point on the circle.
A chord is a segment whose endpoints are on the circle.
A diameter is a chord that contains the center.
A secant is a line that a circle at two points.
A tangent is a line that intersects the circle at one point (point of tangency).
A common tangent is a line, ray or segment that is tangent to two coplanar circles.
Tangents to Circles
Examples:
- You are standing 14 feet from a water tower. The distance from you to the point of tangency on the tower is 28 feet. What is the radius of the water tower?
- AB is a tangent to circle C at B. AD is a tangent to circle C at D. Find the value of x.
How to find angles in diagrams involving tangents and circles?
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.