Right Triangles, Acute Triangles and Obtuse Triangles
Classify Triangles by length of sides
More about Triangles
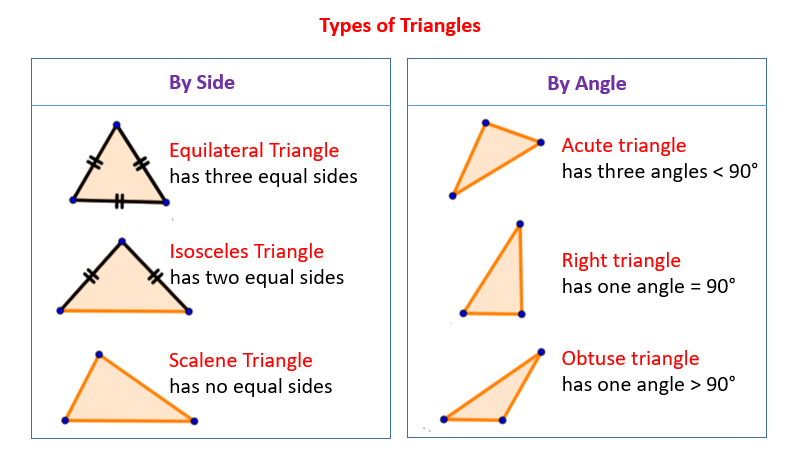
In these lessons, we will learn how to classify triangles by their angles: Right Triangles, Acute Triangles, Obtuse Triangles.
We can also classify triangles by the lengths of their sides.
Triangles classified by their angles
Triangles are polygons that have three sides, three vertices and three angles. One way to classify triangles is by the measure of their angles.The following diagrams show the types of triangle based on sides. Scroll down the page for more examples and solutions of types of triangles.
Right Triangles
A right triangle is a triangle where one of its angles is a right angle (i.e. 90°). The other two angles are acute angles.
You may have noticed that the side opposite the right angle is always the triangle's longest side. It is called the hypotenuseof the triangle. The other two sides are called the legs.
Right triangles are used in many branches of mathematics. For example, in trigonometry and also in the Pythagorean Theorem. The lengths of the sides of a right triangle are related by the Pythagorean Theorem. There are also special right triangles where the sides are of certain fixed ratios.
A right triangle can be isosceles if the two legs are equal in length. A right isosceles triangle will have a 90º angle and two 45º angles.
A right triangle can not be equilateral because the hypotenuse must always be longer than the legs.
Acute Triangles
An acute triangle is a triangle whose angles are all acute (i.e. less than 90°).
In the acute triangle shown below, a, b and c are all acute angles.
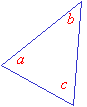
An equilateral triangle is always an acute triangle since all its angles are 60° which are acute angles.
Obtuse Triangles
An obtuse triangle has one obtuse angle (i.e. greater than 90°). The longest side is always opposite the obtuse angle. In the obtuse triangle shown below, a is the obtuse angle.
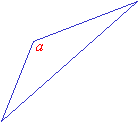
Since the sum of all the angles in a triangle is 180º, only one angle in the triangle can be an obtuse angle , the other two angles must be acute angles.
Discover the six ways to classify triangles, both based on the measure of their side lengths and by the measure of their angles The differences between the acute triangle, the right triangle and the obtuse triangle How to classify triangles - acute, obtuse, right? The Three Types of Triangles (Based on What Kinds of Angles They Have)Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.