Geometry: Quadrilaterals
Related Pages
Angles In A Quadrilateral
Cyclic Quadrilaterals
Polygons
More Geometry Lessons
In these lessons, we will learn
- quadrilaterals.
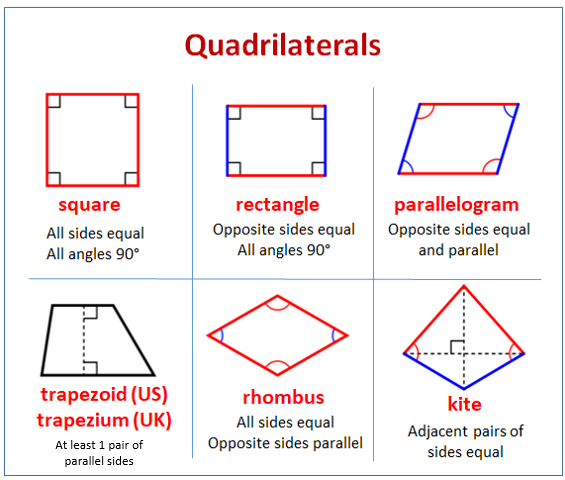
- types of quadrilaterals: parallelogram, rhombus, rectangle, square, kite, trapezoid (trapezium).
What Is A Quadrilateral?
Quadrilaterals are two-dimensional four-sided polygons on a plane.
Quadrilaterals have the following properties:
- four sides,
- two diagonals,
- four internal angles (or vertices),
- the interior angles add up to 360°.
The following diagram shows the properties of some quadrilaterals: square, rectangle, parallelogram, trapezoid, rhombus, kite. Scroll down the page for more examples on the properties of a quadrilaterals.
-
Polygon Worksheets
Printable
Recognizing 2D Shapes (Kindergarten)
Recognizing 3D Shapes (Kindergarten)
Drawing 2D Shapes (Kindergarten)Sides & Corners (First Grade)
2D Shapes (First Grade)
Divide Shapes (Halves & Quarters)Shapes & Attributes (2nd Grade)
Polygons (2nd Grade)
Quadrilaterals (2nd Grade)
Composite Shapes (2nd Grade)
Divide Composite Shapes (2nd Grade)
Divide Circles & Rectangles
Relate Square to Cube (2nd Grade)Classify Quadrilaterals (3rd Grade)
Classify Polygons (3rd Grade)Lines of Symmetry
Types of Triangles
Classify Quadrilaterals (4th & 5th Grade)Online
Quadrilateral Properties
Angles in a QuadrilateralAngles in Polygons
Interior Angles in Polygons
Exterior Angles in Polygons
A convex quadrilateral has all interior angles less than 180°.
A concave quadrilateral has at least one interior angle greater than 180°. (memory tool: concave has a "cave" in it)
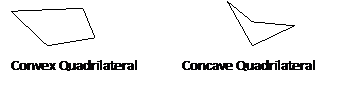
Angles In A Quadrilateral Worksheet
Types Of Quadrilaterals
We will describe the following types of quadrilaterals: parallelogram, rhombus, rectangle, square, trapezoid, kite and trapezium.
Parallelogram
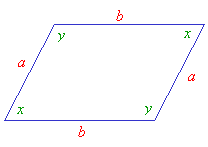
A parallelogram is a four-sided polygon that has the following properties:
- opposite sides are parallel,
- opposite sides are equal,
- opposite angles are equal,
- diagonals bisect each other.
 |
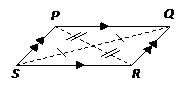 |
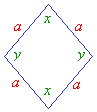
Rhombus
A rhombus is a four-sided polygon that has the following properties:
- opposite sides are parallel,
- all four sides are equal,
- opposite angles are equal,
- diagonals bisect each other at right angles,
- two lines of symmetry (which are the diagonals).
A rhombus is a special case of a parallelogram with four equal sides.
 |
 |
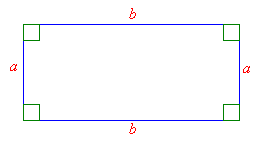
Rectangle
A rectangle is a four-sided polygon that has the following properties:
- opposite sides are parallel,
- opposite sides are equal,
- its angles are all right angles (i.e. 90°),
- diagonals bisect each other,
- diagonals are equal,
- two lines of symmetry.
A rectangle is a special case of a parallelogram with all angles equal to 90°.

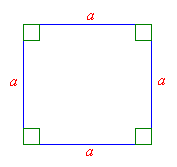
Square
A square is a four-sided polygon that has the following properties:
- opposite sides are parallel,
- all sides are equal,
- its angles are all right angles (i.e. 90°),
- diagonals bisect each other,
- diagonals are equal,
- four lines of symmetry.
A square is a special case of a rectangle in which all the sides are equal.
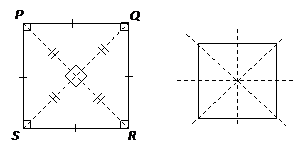
Take note that a diagonal of a square makes two 45°-45°-90° triangles with the sides of the square. Therefore, when given the length of a side, you will be able to work out the length of the diagonal. Or when given the length of the diagonal, you will be able to figure out the length of the side.
Trapezoid
There are two possible definitions for trapezoids.
A trapezoid is a four-sided polygon that has exactly one pair of opposite sides parallel. Using this definition, a parallelogram would not be considered a trapezoid.
A trapezoid is a four-sided polygon that has at least one pair of opposite sides parallel. Using this definition, a parallelogram is a special case of a trapezoid.
A trapezoid is also called a trapezium (UK English).
 |
 |
| p is parallel to q | l is parallel to m |
An isosceles trapezoid has the following properties:
- the two non-parallel sides are equal in length,
- the base angles are equal.
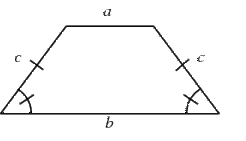
A right trapezoid is a trapezoid with two right angles.

Kite
A kite is a four-sided polygon that has the following properties:
- two pairs of adjacent sides equal,
- one pair of opposite angles equal,
- longer diagonal bisects the shorter diagonal at right angles,
- one line of symmetry.
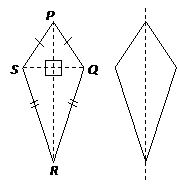
Trapezium
A trapezium represents a different shape depending on whether you are in the US or not.
In the US, a trapezium is a quadrilateral that has no parallel sides.
(Outside the US, a quadrilateral that has no parallel sides is called an irregular quadrilateral.)
Outside the US, a trapezium is a quadrilateral that has a pair of parallel sides.
(In the US, this quadrilateral is called a trapezoid.)
Worksheet on Properties of Quadrilaterals
How to identify and classify quadrilaterals given some properties
Overview of quadrilaterals
Convex quadrilaterals, Concave Quadrilaterals, trapezoid, parallelograms, rectangles, rhombi and squares.
Quadrilaterals: classifying and the sum of their angles
Identify Special Quadrilaterals using a tree diagram
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.