Angles of Polygons

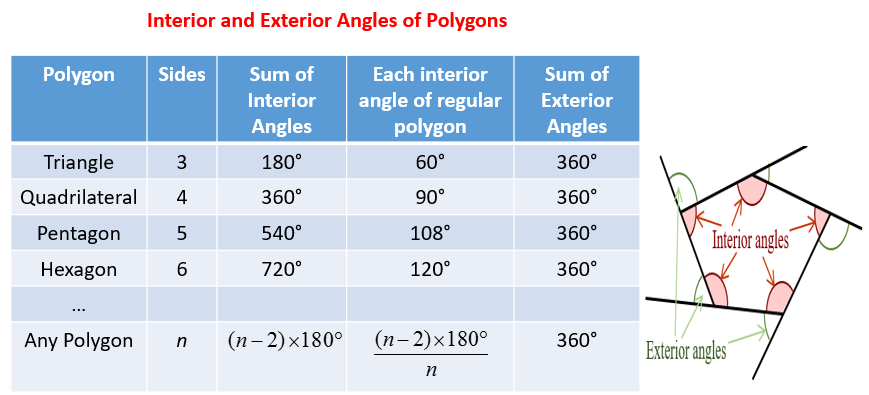
The following diagrams give the formulas for the sum of the interior angles of a polygon and the sum of exterior angles of a polygon. Scroll down the page if you need more examples and explanation.

Printable & Online Geometry Worksheets

Sum Of Interior Angles Of A Polygon

We first start with a triangle (which is a polygon with the fewest number of sides). We know that

The sum of interior angles in a triangle is 180°.

This is also called the Triangle Sum Theorem. Click here if you need a proof of the Triangle Sum Theorem.

Next, we can figure out the sum of interior angles of any polygon by dividing the polygon into triangles. We can separate a polygon into triangles by drawing all the diagonals that can be drawn from one single vertex.

In the quadrilateral shown below, we can draw only one diagonal from vertex A to vertex B. So, a quadrilateral can be separated into two triangles.

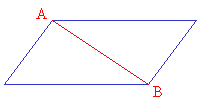
The sum of angles in a triangle is 180°. Since a quadrilateral is made up of two triangles the sum of its angles would be 180° × 2 = 360°

The sum of interior angles in a quadrilateral is 360º

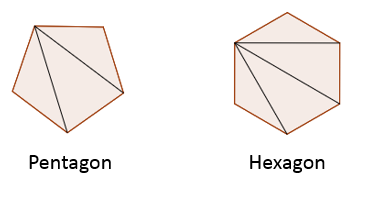
A pentagon (five-sided polygon) can be divided into three triangles. The sum of its angles will be 180° × 3 = 540°

The sum of interior angles in a pentagon is 540°.

A hexagon (six-sided polygon) can be divided into four triangles. The sum of its angles will be 180° × 4 = 720°

The sum of interior angles in a hexagon is 720°.

Formula For The Sum Of Interior Angles

We can see from the above examples that the number of triangles in a polygon is always two less than the number of sides of the polygon. We can then generalize the results for a n-sided polygon to get a formula to find the sum of the interior angles of any polygon.

The following diagram shows the formula for the sum of interior angles of an n-sided polygon and the size of an interior angle of a n-sided regular polygon. Scroll down the page for more examples and solutions on the interior angles of a polygon.

Example:
Find the sum of the interior angles of a heptagon (7-sided)

Solution:
Step 1: Write down the formula (n - 2) × 180°

Step 2: Plug in the values to get (7 - 2) × 180° = 5 × 180° = 900°

Answer: The sum of the interior angles of a heptagon (7-sided) is 900°.

Example:
Find the interior angle of a regular octagon.

Solution:
Step 1: Write down the formula

Step 2: Plug in the values to get

Answer: Each interior angle of an octagon (8-sided) is 135°.

Worksheet using the Formula for the Sum of Interior Angles

How to find the sum of the interior angles of any polygon using triangles and then derive the generalized formula?

• Show Video Lesson

Problems Using The Sum Of Interior Angles

How to find a missing angle using the sum of interior angles of a polygon?

• Show Video Lesson

How to use the sum of interior angles to write an equation and solve for the unknown?
Write an equation and solve for the unknown. Substitute your answer into each expression to determine the measure of the angle. Give reasons for your answers.

• Show Video Lesson

• Show Video Lesson

Formula For The Sum Of Exterior Angles

The sum of exterior angles of any polygon is 360°.

The exterior angle of a regular n-sided polygon is 360°/n

Worksheet using the formula for the sum of exterior angles

Worksheet using the formula for the sum of interior and exterior angles

How to find the sum of the exterior angles and interior angles of a polygon?
Every convex polygon has interior and exterior angles. The interior angles are inside the polygon formed by the sides. The exterior angles form a linear pair with the interior angles.

Example:
Determine the measure of each exterior and interior angle of a regular polygon.

• Show Video Lesson

Problems using the sum of exterior angles

The following video shows a problem involving the sum of exterior angles of a polygon.

Example:
A regular polygon has an exterior angle that measures 40°. How many sides does the polygon have?

• Show Video Lesson

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.