Triangle Sum Theorem
Related Pages
Angles In A Triangle
More Geometry Lessons
Geometry Worksheets
In these lessons, we will learn
- the Triangle Sum Theorem (with worksheets)
- how to prove the Triangle Sum Theorem
- how to solve problems using the Triangle Sum Theorem
Triangle Sum Theorem
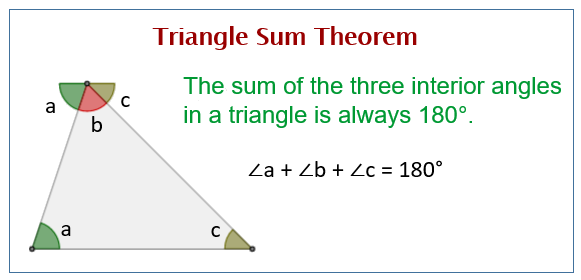
The Triangle Sum Theorem (also called the Angle Sum Property of a Triangle) states that:
The sum of the three interior angles of any triangle is always 180°.
The following diagram shows the Triangle Sum Theorem. Scroll down the page for examples and solutions using the Triangle Sum Theorem.
Geometry Worksheets
Practice your Geometry skills with the following worksheets:
Printable & Online Geometry Worksheets
The Triangle Sum Theorem states that
The sum of the three interior angles in a triangle is always 180°.
The Triangle Sum Theorem is also called the Triangle Angle Sum Theorem or Angle Sum Theorem.
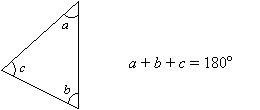
Example:
Find the value of x in the following triangle.
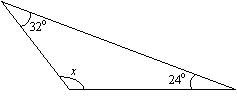
Solution:
x + 24° + 32° = 180° (sum of angles is 180°)
x + 56° = 180°
x = 180° – 56° = 124°
Worksheet 1,
Worksheet 2 using Triangle Sum Theorem
Proof of the Triangle Sum Theorem
How to prove that the sum of the angles of a triangle is 180 degrees (Triangle Sum Theorem)?
This is a two-column proof that involves parallel lines and the alternate angle theorem.
How to prove the Triangle Sum Theorem using right triangles?
We will start with right triangles, and then expand our proof later to include all triangles.
Solving problems using the Triangle Sum Theorem
The following videos show more examples of how to solve problems related to the triangle sum theorem using Algebra.
How to Find the Missing Angle in a Triangle Using the Triangle Sum Theorem?
Step 1. Write out the equation by adding all the angles and making them equal to 180°
Step 2. Solve for x.
Step 3: Substitute to find the missing angles.
Use the triangle sum theorem to find the base angle measures given the vertex angle in an isosceles triangle
Solve for angles using the Triangle Sum Theorem
Example:
Using the diagram shown, find the value of x and the measure of each missing angle in the triangle.
Triangle Properties
Example:
Find the values of x and y for a given triangle problem. This problem uses the Triangle Sum Theorem and the Corollary to the Triangle Sum Theorem.
Triangle Properties
Example:
Find the values of x and y for a given triangle problem. This problem involves linear pair angles as well as the Triangle Sum Theorem.
Solve for angles using the Triangle Sum Theorem and ratios
Example:
The measures of the angles of a triangle are in the ratio 2:5:8. Find the measure of each angle.
Applications of the Triangle Sum Theorem:
- Finding missing angles: If you know two angles of a triangle, you can always find the third.
- Solving algebraic problems: Angles can be expressed in terms of variables, and the theorem helps set up equations to solve for those variables.
- Proving other geometric theorems: It’s a foundational theorem used in many other proofs in geometry.
- Understanding polygons: The formula for the sum of interior angles of any polygon (S=(n−2)×180°) is derived from the fact that any polygon can be divided into triangles.
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.