Algebra: Consecutive Integer Problems

Related Pages
Integers Word Problems
Consecutive Integer Word Problems
Consecutive Integers 2
Consecutive Even Integer Problems
Consecutive Odd Integer Problems
More Algebra Word Problems

What Are Consecutive Integers?

Consecutive integers are integers that follow in sequence, each number being 1 more than the previous number, represented by n, n + 1, n + 2, n + 3, …, where n is any integer.
For example: 23, 24, 25, …

If we start with an even number and each number in the sequence is 2 more than the previous number then we will get consecutive even integers.
For example: 16,18, 20, …

If we start with an odd number and each number in the sequence is 2 more than the previous number then we will get consecutive odd integers.
For example: 33, 35, 37, …

The following diagram shows an example of a consecutive integer problem. Scroll down the page for more examples and solutions on consecutive integer problems.

• Algebra Worksheets

  Words to Equations
  Algebra Word Problems
  Angle Word Problems (6th Grade)
  Angle Word Problems (7th Grade)
  

  Inequality Word Problems
  

  Word Problems (Multiplication & Division)
  2-Step Word Problems (Multiply/Divide/Add/Subtract)
  Multi-step Word Problems (using +, -, ×)
  

Consecutive Integer Problems

Consecutive integer problems are word problems that involve consecutive integers.

The following are common examples of consecutive integer problems.

Example:
The sum of the least and greatest of 3 consecutive integers is 60. What are the values of the 3 integers?

Solution:
Step 1: Assign variables:
Let x = least integer
x + 1 = middle integer
x + 2 = greatest integer

Translate sentence into an equation.
Sentence: The sum of the least and greatest is 60.
Rewrite sentence:
x + (x + 2) = 60

Step 2: Solve the equation
Combine like terms
2x + 2 = 60

Isolate variable x
2x = 58

Step 3: Check your answer
29 + 29 + 2 = 60
The question wants all the 3 consecutive numbers: 29, 30 and 31

Answer: The 3 consecutive numbers are 29, 30 and 31.

Consecutive Odd Integers

Example 2:
The lengths of the sides of a triangle are consecutive odd numbers. What is the length of the longest side if the perimeter is 45?

Solution:
Step 1: Being consecutive odd numbers we need to add 2 to the previous number.
Assign variables:
Let x = length of shortest side
x + 2 = length of medium side
x + 4 = length of longest side

Sketch the figure

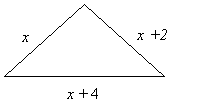
Step 2: Write out the formula for perimeter of triangle.
P = sum of the three sides

Step 3: Plug in the values from the question and from the sketch.
45 = x + x + 2 + x + 4

Combine like terms
45 = 3x + 6

Isolate variable x
3x = 45 – 6
3x = 39
x =13

Step 3: Check your answer
13 + 13 + 2 + 13 + 4 = 45

Be careful! The question requires the length of the longest side.
The length of longest = 13 + 4 =17

Answer: The length of longest side is 17

Consecutive Even Integers

Example 3:
John has a board that is 5 feet long. He plans to use it to make 4 shelves whose lengths are to be a series of consecutive even numbers. How long should each shelf be in inches?

Solution:
Step 1: Being consecutive even numbers we need to add 2 to the previous number.
Assign variables:
Let x = length of first shelf
x + 2 = length of second shelf
x + 4 = length of third shelf
x + 6 = length of fourth shelf

Step 2: Convert 5 feet to inches
5 × 12 = 60

Step 3: Sum of the 4 shelves is 60
x + x + 2 + x + 4 + x + 6 = 60

Combine like terms
4x + 12 = 60

Isolate variable x
4x = 60 – 12
4x = 48
x = 12

Step 3: Check your answer
12 + 12 + 2 + 12 + 4 + 12 + 6 = 60

The lengths of the shelves should be 12, 14, 16 and 18.

Answer: The lengths of the shelves in inches should be 12, 14, 16 and 18.

How to find consecutive integers, consecutive odd integers, or consecutive even integers that add up to a given number

Examples:

1. The sum of three consecutive integers is 657; find the integers.
2. The sum of two consecutive integers is 519; find the integers.
3. The sum of three consecutive even integers is 528; find the integers.
4. The sum of three consecutive odd integers is 597; find the integers.

• Show Video Lesson

The following video shows how to solve the integer word problems.

Examples:

1. The sum of two consecutive integers is 99. Find the value of the smaller integer.
2. The sum of two consecutive odd integers is 40. What are the integers?
3. The sum of three consecutive even integers is 30. Find the integers.

• Show Video Lesson

How to solve consecutive integer word problems?

Example:
The sum of three consecutive integers is 24. Find the integers.

• Show Video Lesson

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.