Consecutive Odd Integer Problems
In these lessons, we will learn how to solve consecutive odd integer problems.
Related Pages
Integers Word Problems
Consecutive Even Integer Problems
Consecutive Integer Word Problems
Consecutive Integers 2
More Algebra Word Problems
Integer worksheets
Consecutive Integers
Consecutive integer problems are word problems that involve consecutive integers.
Consecutive integers are integers that follow in sequence, each number being 1 more than the previous number, represented by n, n +1, n + 2, n + 3, …, where n is any integer. For example: 23, 24, 25, …
If we start with an even number and each number in the sequence is 2 more than the previous number then we will get consecutive even integers. For example: 16,18, 20, …
If we start with an odd number and each number in the sequence is 2 more than the previous number then we will get consecutive odd integers. For example: 33, 35, 37, …
The following are some examples of consecutive odd integer problems. Scroll down the page for more examples and solutions on consecutive odd integers.
Example:
The lengths of the sides of a triangle are consecutive odd numbers. What is the length of the longest side if the perimeter is 45?
Solution:
Step 1: Being consecutive odd numbers we need to add 2 to the previous number.
Assign variables:
Let x = length of shortest side
x + 2 = length of medium side
x + 4 = length of longest side
Step 2: Sketch the figure
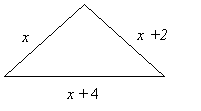Step 2: Write out the formula for perimeter of triangle.
P = sum of the three sides
Step 3: Plug in the values from the question and from the sketch.
45 = x + x + 2 + x + 4 Combine like terms 45 = 3x + 6 Isolate variable x 3x = 45 – 6
3x = 39
x = 13
Step 4: Check your answer
13 + 13 + 2 + 13 + 4 = 45
Be careful! The question requires the length of the longest side.
The length of longest = 13 + 4 =17
Answer: The length of longest side is 17
How the solve the integer word problem?
Example:
The sum of three consecutive odd integer is 231. What is the largest integer?.
How to find consecutive even and odd numbers given the sums?
Examples:
- Find three consecutive even numbers whose sum is 84
- Find four consecutive odd numbers whose sum is 152
Consecutive Odd Integer Problem
Example:
The product of two consecutive odd integers is 99. What are the numbers?
Consecutive Odd Integers - Hard
Example:
Find three consecutive odd integers so that the sum of twice the first, the second and three times the third is 152.
Find Integers That Are Consecutive, Consecutive Even, or Consecutive Odd
This video goes through examples of finding consecutive integers, consecutive odd integers, & consecutive even integers that add up to a given number.
Examples:
- The sum of three consecutive integers is 657; find the integers.
- The sum of three consecutive odd integers is 597; find the integers.
- The sum of three consecutive even integers is 528; find the integers.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.