Algebra: Isolate A Variable (Transposition)

How To Isolate A Variable?

Transposition is a method to isolate the variable to one side of the equation and everything else to the other side so that you can solve the equation.

Two methods are covered here:

• Method 1: Using inverse operations
• Method 2: a shortcut trick that allows you to work faster

The following table gives the steps to Isolate a Variable. Scroll down the page for examples and solutions.

Printable & Online Algebra Worksheets

Method 1

A quick review of the basic principles - all equations have two sides: a Left Side (LS) and a Right Side (RS). The common transposition method is to do the same thing (mathematically) to both sides of the equation, with the aim of bringing like terms together and isolate the variable (or the unknown quantity).

For Example:
5x + 8 = 3x – 6

We want to get rid of the number 8 from the left side.
So we subtract 8 from both sides of the equation.

5x + 8	=	3x – 6	original equation
– 8	=	– 8	subtract 8 from both sides
5x	=	3x – 14	resulting equation

Next, we want to get rid of 3x from the right side.
So, we subtract 3x from both sides of the equation.

5x	=	3x – 14	result from above
– 3x	=	– 3x	subtract 3x from both sides
2x	=	– 14	resulting equation

Now, we want to get rid of the coefficient 2.
So, we divide 2 from both sides of the equation.

2x	=	– 14	result from above
÷2	=	÷2	divide both sides by 2
x	=	– 7	resulting solution

Check the Answer
Now check your answer x = –7 by plugging it back into the original equation.

5x + 8 = 3x – 6

LS: 5 × (– 7) + 8 = – 35 + 8 = – 27
RS: 3 × (– 7) – 6 = – 21 – 6 = – 27

LS = RS, ∴ answer is correct.

Algebra: How to solve equations by isolating the variable?

An equation is a symbolic statement that two algebraic expressions are equal.
To solve an equation means to find the variable or unknown.
The rule is that the same operation must be done on both sides of the equation to preserve equality.

Examples:

1. x + 4 = 20
   
2. x - 4 = 20
   
3. 4x = 20
   
4. x/4 = 20
   Isolate the variable:
5. 5x - x = 20 + 4
   
6. 9 - 4x = 8x
   
7. 8 - 5x - x = 14

• Show Video Lesson

How to isolate a variable and solve linear equations (variables on both sides of the equation)?

Example:
Solve for y and check your solution
20 - 7y = 6y - 6

• Show Video Lesson

How to isolate the variable using inverse operations to solve fraction equations?

Examples:
a + 1/2 = 4
3/7 + n = 2 2/5
5/7 x = 4 2/3
3/4 b = -24

• Show Video Lesson

How to isolate a variable in a formula?

1. 2p = kx - q, isolate for x
2. (3b -4)/2 = C, isolate for b

• Show Video Lesson

How to isolate a variable when the variable or expression is in the denominator?

1. 8/y = 3
   
2. (x + 3)/(x + 5) = 20
   
3. 5/(x + 3) = 4/(x + 4)

• Show Video Lesson

Transposition (Rearranging Equations) - Introduction

What is transposition? What is it used for?

• Show Video Lesson

Method 2

In this method we isolate the variable by moving like terms to one side of the equation. To maintain the equality of the equation, when removing a term from one side of the equation we perform the opposite operation to the other side.

For example:
5x + 8 = 3x – 6

To remove + 8 from the LS, we subtract 8 from the RS.

To remove + 3x from the RS, we subtract 3x from the LS.

To remove the coefficient 2, we divide 2 on the RS.

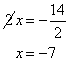
When you have grasped Method 2, it is faster because it allows you to perform several steps at the same time to isolate the variable.

For example:
5x + 8 = 3x – 6

Shortcut Trick to help you solve equations (Variable on one side)

Examples:

1. (3x + 5)/7 = 2
2. (5x - 8)/3 = 4
3. \(\sqrt {{x^2} + 7} + 5 = 9\)
4. \(\frac{{\sqrt {2x} }}{2} = 2\)
5. \(\frac{{\sqrt {5x - 6} \times 4}}{2} = 6\)

• Show Video Lesson

Shortcut Trick to help you solve equations (Variables on both sides)

Examples:

1. 3x + 4 = 2x + 6
2. 2x + 1 = 4x - 9
3. x - 3 = 4x + 6

• Show Video Lesson

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.