Algebra: Simplifying Equations

Simplifying equations is often the first step to solving algebra equations. Some methods that can be used to simplify an equation are:

Combine Like Terms
Multiplication and Division of Terms
Removal of Brackets - Distributive Property
Cross Multiplication

Combine Like Terms

Like terms are terms that have the same variable part i.e. they only differ in their coefficients. Combining like terms is very often required in the process of simplifying equations.

For example:

2x and –5x are like terms
a and are like terms
6x and 5y are unlike terms

Like terms can be added or subtracted from one another.

For example:

a + a = 2 × a = 2a    (We usually write 2 × a as 2a)
2a + 4a = 6a
a + a + a = 3a
2a + 4      (Unlike terms cannot be simplified)
4a + 3b    (Unlike terms cannot be simplified)
6a – 3a = 3a
8b – 8b = 0
5a – 3      (Unlike terms cannot be simplified)
6a – 4b    (Unlike terms cannot be simplified)

Example 1:

Simplify: 8xy – 5yx = 1

Solution:

Step 1: 5yx is the same as 5xy using the commutative property

Step 2: Since the right side is already simple, we can work on the left side expression:

8xy – 5yx = 8xy – 5xy = 3xy
Putting back the left side and right side of the equation:
3xy = 1

Answer: 3xy = 1

Example 2:

Simplify: 7a + 5b – 6b + 8a + 2b = 0

Solution:

Step 1: Group together the like terms:

7a + 5b – 6b + 8a + 2b = 0
(7a + 8a) + (5b – 6b + 2b) = 0

Step 2: Then simplify:

15a + b = 0

Answer: 15a + b = 0

How to Solve an Equation by Combining Like Terms?

• Show Step-by-step Solutions

Multiplication and Division of Terms

The coefficients and variables of terms can be multiplied or divided together in the process of simplifying equations.

For example:

3 × 4b = 3 × 4 × b = 12b

5a × 3a = 5 × a × 3 × a = 5 × 3 × a × a = 15a²    (using exponents)

Beware!	a × a = a2
	a + a = 2a

Example 1:

Simplify: 4a × 5a ÷ 2a = 60

Solution:

Step 1: Perform the multiplication and division

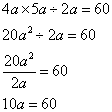
Step 2: Isolate variable a

Answer: a = 6

Solving Equations using Multiplication or Division

• Show Step-by-step Solutions

Removal of Brackets - Distributive Property

Sometimes removing brackets (parenthesis) allows us to simplify the expression. Brackets can be removed by using the distributive property. This is often useful in simplifying equations.

For example:

3(a – 3) + 4 = 3 × a + 3 × (-3) + 4 = 3a – 9 + 4 = 3a – 5

5 – 6 (b + 1) = 5 + ( – 6 ) × b + (– 6) × 1 = 5 – 6b – 6 = – 6b – 1

Example 1:

Simplify: 5(a – 4) + 3 = 8

Solution:

Step 1: Remove the brackets

5a – 20 + 3 = 8

Step 2: Isolate variable a

5a = 8 – 3 + 20
5a = 25

Answer: a = 5

How to Solve an Equation by the Distributive Property?

• Show Step-by-step Solutions

Cross Multiplication

Cross multiplication allows you to remove denominators from fractions in an equation. Note that this technique applies only towards simplifying equations, not to simplifying expressions.

For example, if you have the equation:

then you can multiply the numerator of one fraction with the denominator of the other fraction (across the = sign) as shown:

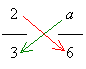
to obtain the equation

(2 × 6) = a × 3

Example 1:

Simplify:

Solution:

Step 1: Cross Multiply

4 × a = 8 × 5
4a = 40

Step 2: Isolate variable a

Answer: a = 10

Solve equations easily by cross-multiplying when there are two fractions

• Show Step-by-step Solutions

Check out our most popular games!

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.