Vector Addition
In these lessons, we will learn
- how to add vectors geometrically using the ‘nose-to-tail’ method or "head-to-tail" method or triangle method,
- how to add vectors using the parallelogram method,
- that vector addition is commutative,
- that vector addition is associative,
- how to add vectors using components.
Related Pages
Vectors
Equal Vectors
Vector Subtraction
Vector Multiplication
Vector Geometry
The following diagrams show how to add vectors graphically using the Triangle or Head-to-Tail Method and the Parallelogram Method. Scroll down the page for more examples and solutions.
"Nose-to-Tail" Method
Vectors can be added using the ‘nose-to-tail’ method or "head-to-tail" method.
Two vectors a and b represented by the line segments can be added by joining the ‘tail’ of vector b to the ‘nose’ of vector a. Alternatively, the ‘tail’ of vector a can be joined to the ‘nose’ of vector b.
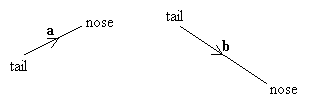
Example:
Find the sum of the two given vectors a and b.
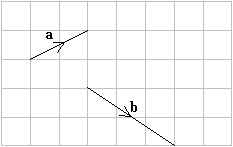
Solution:
Draw the vector a. Draw the ‘tail’ of vector b joined to the ‘nose’ of
vector a The vector a + b is from the ‘tail’ of a to the ‘nose’ of b.
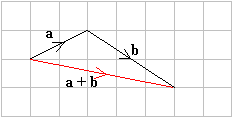
Example:
Given that 
, find the sum of the vectors.
Solution:
Triangle Law of Vector Addition
In vector addition, the intermediate letters must be the same. Since PQR forms a triangle, the rule is also called the triangle law of vector addition.
Graphically we add vectors with a “head to tail” approach.
The addition of vectors using the head-to-tail method.
Parallelogram Law of Vector Addition
Vectors can be added using the parallelogram rule or parallelogram law or parallelogram method.
Graphical Method of Vector Addition (Parallelogram Method).
How to add and subtract vectors at any angle?
Includes parallelogram method and worked examples.
How to add vectors by scale drawing?
- Choose a scale
- Draw the vectors so the tip of one vector is connected to the tail of the next
- Make sure the length and direction of each arrow is correct.
How to add vectors by the parallelogram method?
The resultant is the diagonal starting from the joined tails.
When adding two vectors, the biggest resultant possible is when the vectors are parallel.
Two methods used to add vectors graphically: "Tail-to-tip" method and parallelogram method
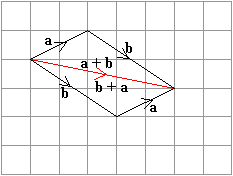
Vector Addition is Commutative
We will find that vector addition is commutative, that is a + b = b + a
This can be illustrated in the following diagram.
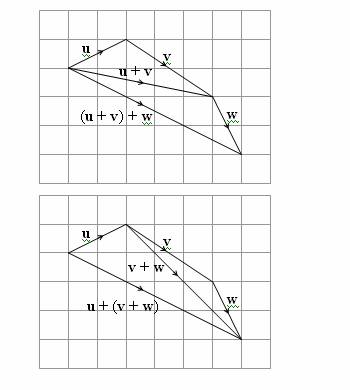
Vector Addition is Associative
We also find that vector addition is associative, that is (u + v) + w = u + (v + w).
This can be illustrated in the following two diagrams. Notice that (u + v) + w and u + (v + w) have the same magnitude and direction and so they are equal.
Example:
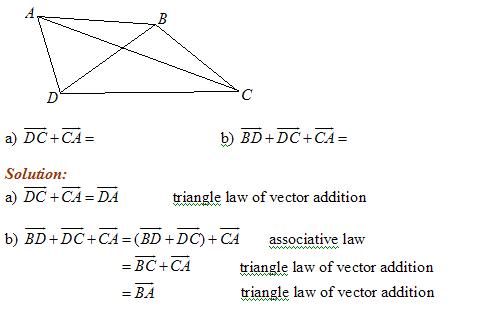
ABCD is a quadrilateral. Simplify the following:
Add Vectors using components
Vectors are added by adding the corresponding components.
How to Add vectors using components (part 1)
An example of how to add two vectors by using their components. This video goes through breaking them
down, and adding the components.
How to Add vectors using components (part 2)
Vector Word Problems
The following video shows how vector addition can be used to solve word problems.
Example:
A metal ball lies on a flat horizontal surface. It is attracted by two magnets placed around it. The first magnet’s force on the ball is 5N. The second magnet’s force on the ball is 3N in a direction that is a 100° rotation from the first magnet’s force.
- What is the combined strength of the magnet’s pull?
- What is the direction of the magnet’s combined pulls relative to the direction of the first magnet’s pull?
Relative Motion Vector Addition: Physics Challenge Problem
Example:
A tour boat has two hours to take passengers from the start to finish of a tour route. The final
position is located 18.6 km from the start at 26 degrees north of west. There is a current in the
water moving at 6.4 km/hr with a global angle of 255 degrees. What would be the boat’s velocity
(magnitude and direction) relative to the body of water to reach the destination at the correct time?
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.