

Multiply a Vector by a Scalar
A scalar quantity has a magnitude but no direction.
In vectors, a fixed numeric value is called a scalar.
A vector can be multiplied by a scalar.
When a vector x is multiplied by 3, the result is 3x.
When a vector x is multiplied by –2, the result is –2x.
In the above examples, 3 and –2 are scalars.


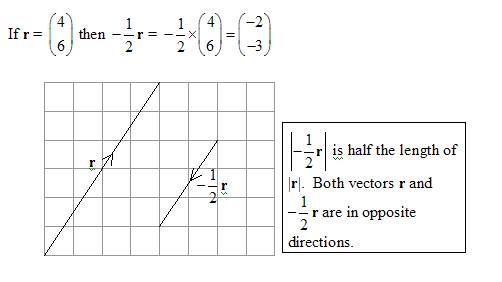
Multiplying a Vector by a Scalar
How to multiply a vector by a scalar including some algebraic properties of scalar multiplication.
Discuss the concept of a linear combination of vectors and shows an example of drawing a geometric sum/difference of 3 vectors.
Multiplying a vector by a scalar (real number) means taking a multiple of a vector.
Two vectors are said to be collinear when they are drawn tail to tail and they lie on the same line.
If a and b are two non-collinear vectors in the plane, then any other vector can be written as a linear combination of a and b.
Properties of Scalar Multiplication
Let v be any vector and k be a scalar. Then kv is a vector and kv is |k| times as long as v.
• If k > 0, kv has the same direction as v.
• If k < 0, kv has the opposite direction as v.
• If k = 0, kv is the zero vector.
Examples:
1. Given the vector 75 km/h [N 50° E] draw twice this vector.
2. OF = 3b and OE = 2a, write each of the following in terms of a and b.
a) EF
b) OG
How to show geometrically what multiplication of a vector by a scalar is?
Understanding multiplying vectors by scalars
Examples:
w = (1,2)
Find 3w
Find -2w
Try out our new and fun Fraction Concoction Game.
Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.



We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.