Hypotenuse, Adjacent & Opposite Sides Of A Right Triangle

Sides Of A Right Triangle

First, identify the right angle. It’s the angle that measures 90 degrees and is usually marked with a small square in the corner.
The hypotenuse is the side opposite the right angle. It’s always the longest side of the right triangle.
The other two sides of the right triangle are called legs.
When you’re working with one of the other two angles in the right triangle (not the right angle itself), you also use the terms “opposite” and “adjacent”:
Opposite: The side across from the angle you’re considering.
Adjacent: The side next to the angle you’re considering (and it’s not the hypotenuse).

Hypotenuse, Adjacent and Opposite Sides.

In the following right triangle PQR,

• the side PQ, which is opposite to the right angle PRQ is called the hypotenuse. The hypotenuse is the longest side of the right triangle.
• the side RQ is called the adjacent side of angle θ.
• the side PR is called the opposite side of angle θ.

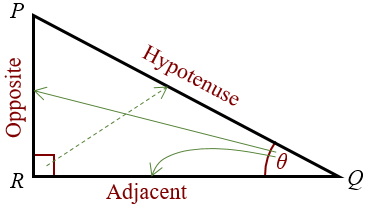
Note: The adjacent and the opposite sides depend on the angle θ. For complementary angle of θ, the labels of the 2 sides are reversed.

Example:
Identify the hypotenuse, adjacent side and opposite side in the following triangle:
a) for angle x
b) for angle y

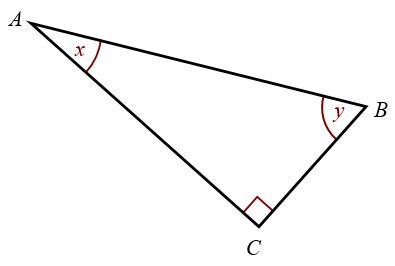
Solution:
a) For angle x: AB is the hypotenuse, AC is the adjacent side , and BC is the opposite side.
b) For angle y: AB is the hypotenuse, BC is the adjacent side , and AC is the opposite side.

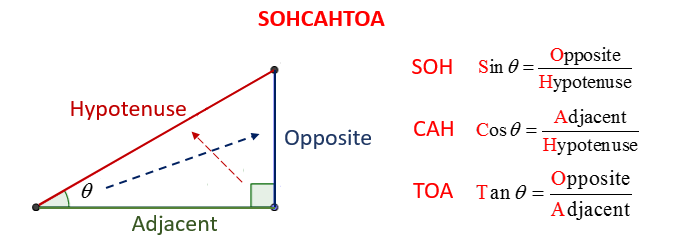
SOH-CAH-TOA

Why are these names important?
These names are essential for trigonometry because they are used in the definitions of the trigonometric functions (sine, cosine, and tangent):
sine(angle) = Opposite / Hypotenuse
cosine(angle) = Adjacent / Hypotenuse
tangent(angle) = Opposite / Adjacent

The following diagram show how to use SOHCAHTOA for a right triangle.

Lots of Printable and Online Trigonometry Worksheets for revision and practice.

How to identify the Opposite Sides, Adjacent Sides and Hypotenuse of a Right Triangle?

Definition of Cos, Sin, Tan, Csc, Sec, Cot for the right triangle
sin x = opposite/hypotenuse
cos x = adjacent/hypotenuse
tan x = opposite/adjacent
csc x = 1/sin x = hypotenuse/opposite
sec x = 1/cos x = hypotenuse/adjacent
cot x = 1/tan x = adjacent/opposite

• Show Video Lesson

Using the Sine Formula (the SOH formula)

The first part of this video will explain the difference between the hypotenuse, adjacent and opposite sides of a right triangle. Then it shows how to use the sine formula (the SOH formula).

Sine = Opposite over the Hypotenuse

• Show Video Lesson

Using the Cosine Formula (the CAH formula)

Cosine = Adjacent over Hypotenuse

• Show Video Lesson

Using the Tangent Formula (the TOA formula)

Tangent = Opposite over Adjacent

• Show Video Lesson

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.