Coordinate Geometry
Related Pages
Coordinate Geometry For GRE
Coordinate Geometry Proofs
More Geometry Lessons
In these lessons, we will learn
- the coordinate plane or Cartesian plane
- the slope formula
- the equation of a line
- the slopes of parallel lines
- the slopes of perpendicular lines
- the midpoint formula
- the distance formula
Coordinate Geometry Formulas
The following table gives some coordinate geometry formulas. Scroll down the page if you need more explanations about the formulas, how to use the formulas and worksheets to practice.
Printable & Online Coordinate Geometry Worksheets
What Is A Coordinate Plane Or Cartesian Plane?
The coordinate plane or Cartesian plane is a basic concept for coordinate geometry. It describes a two-dimensional plane in terms of two perpendicular axes: x and y.
The x-axis indicates the horizontal direction while the y-axis indicates the vertical direction of the plane. In the coordinate plane, points are indicated by their positions along the x and y-axes.
For example: In the coordinate plane below, point L is represented by the coordinates (–3, 1.5) because it is positioned on –3 along the x-axis and on 1.5 along the y-axis. Similarly, you can figure out the positions for the points M = (2, 1.5) and N = (–2, –3).
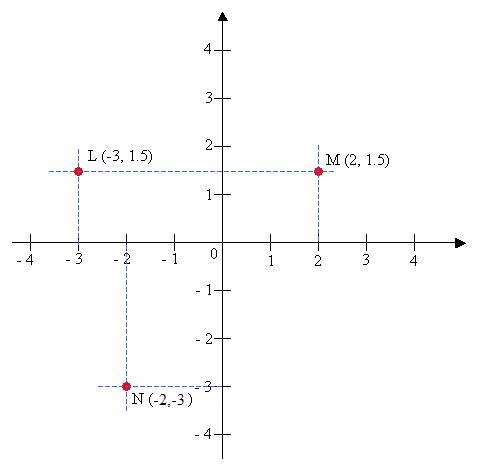
How to plot points in the coordinate plane and how to determine the coordinates of points on the coordinate plane?
To graph or plot points, we use two perpendicular lines called axes. The point at which the axes
cross is called the origin. Arrows in the axes indicate the positive directions.
Consider the ordered pair (4, 3). The numbers in an ordered pair are called the coordinates. The first coordinate or x-coordinate in this case is 4 and the second coordinate or y-coordinate is 3.
To plot the point (4, 3) we start at the origin, move horizontally to the right 4 units, move up vertically 3 units, and then make a point.
Example:
- Plot the following points: A(-3,2), B(-1,4), C(-2,-4), D(0,-2), E(3,0)
- Find the coordinates of the given points
How To Find The Slope Of A Line?
On the coordinate plane, the slant of a line is called the slope. Slope is the ratio of the change in the y-value over the change in the x-value, also called rise over run.
Given any two points on a line, you can calculate the slope of the line by using this formula:
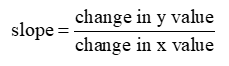
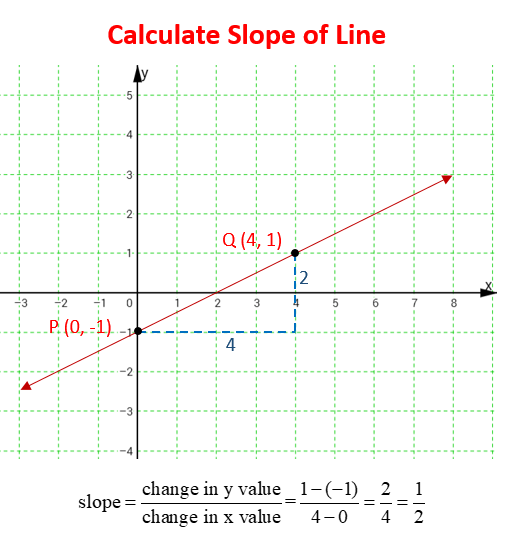
For example: Given two points, P = (0, –1) and Q = (4,1), on the line we can calculate the slope of the line.
What Is The Y-Intercept?
The y-intercept is where the line intercepts (meets) the y-axis.
For example: In the above diagram, the line intercepts the y-axis at (0,–1). Its y-intercept is equals to –1.
What Is The Equation Of A Line?
In coordinate geometry, the equation of a line can be written in the form, y = mx + b, where m is the slope and b is the y-intercept. (mnemonic for this formula
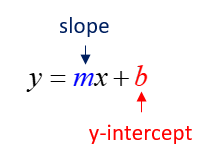
For example: The equation of the line in the above diagram is:
y = ½ x - 1
How To Find The Slope Given 2 Points?
Example: Find the slope of the two points (-6,3) and (4,-3)
How To Write A Slope Intercept Equation For A Line On A Graph?
What Is A Negative Slope?
Let’s look at a line that has a negative slope.
For example: Consider the two points, R(0, 2) and S(6, –2) on the line. What would be the slope of the line? What would be the equation of the line?
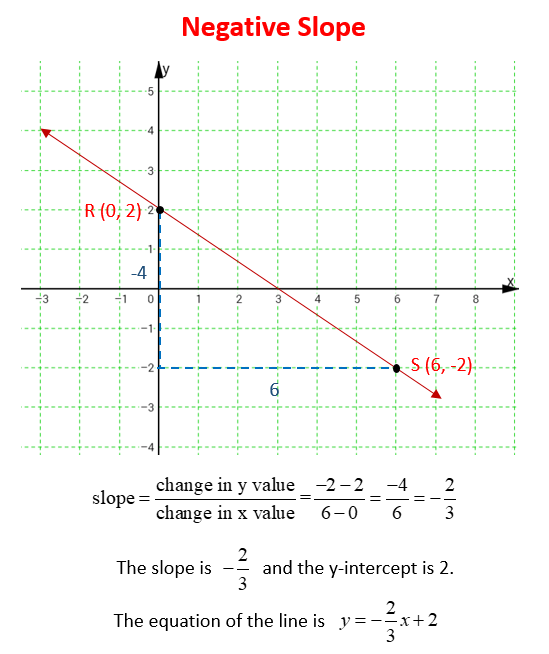
How To Determine The Slope Of A Line Given The Graph Of A Line With A Negative Slope?
How To Find The Slopes Of Parallel Lines?
In coordinate geometry, two lines are parallel if their slopes (m) are equal.
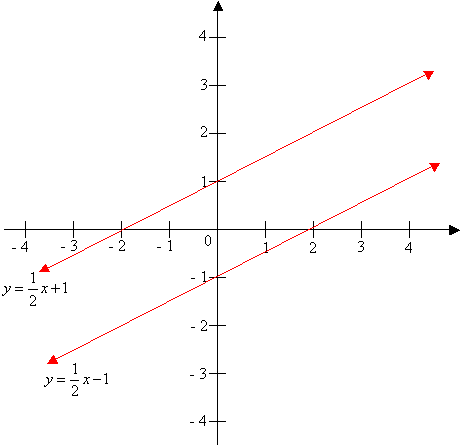
For example: The line y = ½ x - 1 is parallel to the line y = ½ x + 1 because their slopes are both the same.
How to find the equation of a line parallel to a given line and passing through a given point?
Example: Write the equation of a line that is parallel to the line 2x - 4y = 8 and goes through the point (3, 0).
How To Find The Slopes Of Perpendicular Lines?
In the coordinate plane, two lines are perpendicular if the product of their slopes (m) is –1.
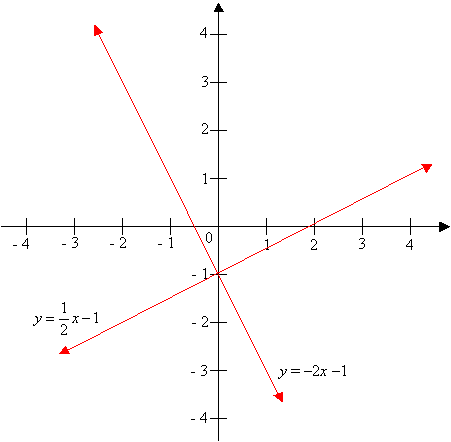
For example: The line y = ½ x - 1 is perpendicular to the line y = –2x – 1. The product of the two slopes is ½ × (-2) = -1.
How to find the slope of a line that is perpendicular to a given line?
Example: Find the slope of the line that is perpendicular to the line 3x + 2y = 6.
What Is The Midpoint Formula?
Some coordinate geometry questions may require you to find the midpoint of line segments in the coordinate plane. To find a point that is halfway between two given points, get the average of the x-values and the average of the y-values.
The midpoint between the two points (x1,y1) and (x2,y2) is
For example: The midpoint of the points A(1,4)
and B(5,6) is
How to derive and use the midpoint formula?
This video gives the formula for finding the midpoint of two points and one example to find the midpoint.
What Is The Distance Formula
In the coordinate plane, you can use the Pythagorean Theorem to find the distance between any two points.
The distance between the two points (x1,y1) and
(x2,y2) is
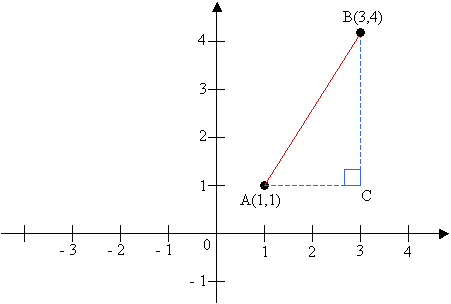
For example: To find the distance between A(1,1) and B(3,4), we form a right angled triangle with A̅B̅ as the hypotenuse. The length of A̅C̅ = 3 – 1 = 2. The length of B̅C̅ = 4 – 1 = 3.
Applying Pythagorean Theorem:
A̅B̅2 = 22 + 32
A̅B̅ = 13
A̅B̅ = √13
How to derive and use the distance formula?
This video shows how the distance formula comes from the Pythagorean Theorem, and one example of
finding the distance between two points.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.