Coordinate Geometry

This lesson is part of a series of lessons for the quantitative reasoning section of the GRE revised General Test. In this lesson, we will learn:

• xy-coordinate system
• four quadrants
• ordered pair
• plot points on the coordinate plane
• reflection of points about the x-axis, y-axis and origin

Coordinate Geometry

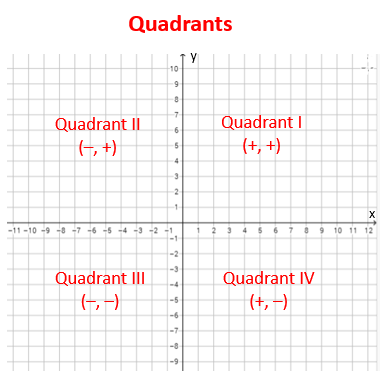
Two real number lines that are perpendicular to each other and that intersect at their respective zero points define a rectangular coordinate system, often called the xy-coordinate system or xy-plane. The horizontal number line is called the x-axis and the vertical number line is called the y-axis. The point where the two axes intersect is called the origin, denoted by O. The positive half of the x-axis is to the right of the origin, and the positive half of the y-axis is above the origin. The two axes divide the plane into four regions called quadrants I, II, III, and IV, as shown in the figure below.

The following diagram shows the four quadrants of the coordinate plane. Scroll down the page for more examples and solutions.

 

Coordinate Geometry Worksheets
Practice your skills with the following worksheets:
Printable & Online Coordinate Geometry Worksheets

Points on the Coordinate Plane

Each point P in the xy-plane can be identified with an ordered pair (x, y) of real numbers and is denoted by P(x, y). The first number is called the x-coordinate, and the second number is called the y-coordinate. A point with coordinates (x, y) is located x units to the right of the y-axis if x is positive or to the left of the y-axis if x is negative. Also, the point is located y units above the x-axis if y is positive or below the x-axis if y is negative. If the point lies on the y-axis, and if the point lies on the x-axis. The origin has coordinates (0, 0). Unless otherwise noted, the units used on the x-axis and the y-axis are the same.

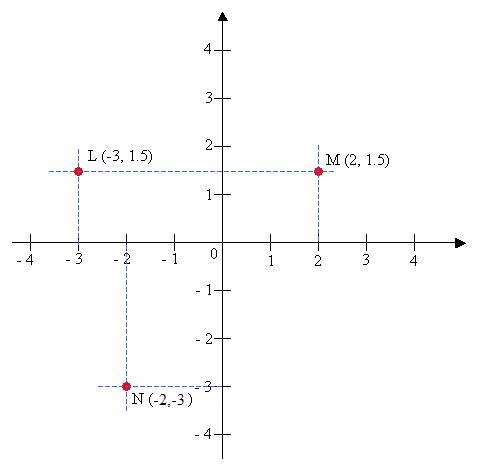
In the following coordinate plane: .
Point M has coordinates (2, 1.5). To get to point M, we move 2 units to the right (positive) and 1.5 units up (positive).
Point L is represented by the coordinates (–3, 1.5). To get to point L, we move 3 units to the left (negative) and 1.5 units up (positive)
Point N has coordinates (–2, –3). To get to point N, we move 2 units to the left (negative) and 3 units down (negative).

Coordinate plane or Cartesian plane, quadrants
How to plot points on the Cartesian plane?

• Show Step-by-step Solutions

How to find the ordered pair or coordinates of a given point?
How to plot the point given the ordered pair or coordinates?

• Show Step-by-step Solutions

Reflection of points about the x-axis, y-axis and origin

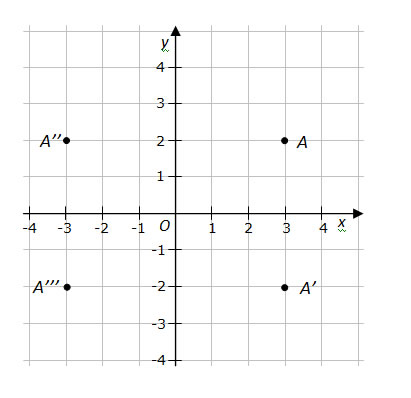
In the diagram below,  the three points A’ (3, −2), A’’ (−3, 2), A’’’ (−3, −2) are geometrically related to A (3, 2)  as follows.
• A’ is the reflection of A about the x-axis, or A’ and A are symmetric about the x-axis.
• A’’ is the reflection of A about the y-axis, or A’’ and A are symmetric about the y-axis.
• A’’’ is the reflection of A about the origin, or A’’’ and A are symmetric about the origin.

Reflect a Point about the x-axis, y-axis, and the Origin
This video provides an example of how to determine the coordinates of a point reflected about the x-axis, y-axis, and the origin.

• Show Step-by-step Solutions

Check out our most popular games!

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.