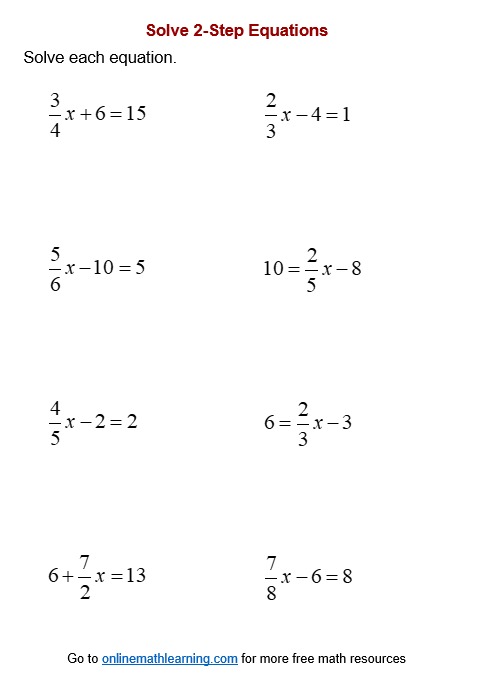Two-Step Equation Worksheets (with Fractions)

“Solving 2-step Equation” worksheets:

• Solve 2-step equations (positive answers)
  
• Solve 2-step equations (negative answers)
  
• Solve 2-step equations (fraction answers)
  
• Solve 2-step equations (with fractions)
  
• Solve 2-step equations (with decimals)
  

Examples, solutions, videos, and worksheets to help Grade 6 and Grade 7 students learn how to solve two-step equations (with fractions)

How to solve two-step equations (with fractions)?

There are three sets of solving two-step equations (with fractions) worksheets.

• Solve 2-step equations (fractional coefficients).
• Solve 2-step equations (fractional constants).
• Solve 2-step equations (fractional coefficients & constants).

These are the steps to solve two-step equations:

1. Determine the operations: Look at the equation and identify the operations being performed on the variable. It could involve addition, subtraction, multiplication, or division.
2. Undo addition or subtraction: Perform the inverse operation of addition or subtraction to isolate the variable term. If there’s addition, subtract the constant term from both sides of the equation. If there’s subtraction, add the constant term to both sides.
3. Undo multiplication or division: Perform the inverse operation of multiplication or division to isolate the variable. If there’s multiplication, divide both sides of the equation by the coefficient of the variable. If there’s division, multiply both sides by the reciprocal of the coefficient.
4. Simplify and solve.
5. Check your solution: After solving the equation, substitute the value back into the original equation to verify if it satisfies the equation. If it does, then you have found the correct solution. If not, review your steps and check for any errors.

Simplify and solve: Simplify both sides of the equation by performing any necessary arithmetic operations. Finally, determine the value of the variable by solving the simplified equation.

Example: Solve the equation 3/4 x + 5 = -16.

1. Determine the operations: The operations involved are addition and multiplication.
2. Undo addition: To isolate the variable term, we need to undo the addition. Subtract 5 from both sides of the equation:
   3/4 x + 5 - 5 = -16 - 5
   3/4 x = -21
   
3. Undo multiplication: To further isolate the variable, we need to undo the multiplication. Divide both sides of the equation by 3/4 or multiply by the reciprocal which is 4/3:
   3/4 x × 4/3 = -21 × 4/3
   x = -28
4. Simplify and solve: The equation is now simplified to x = -28.
5. Check your solution by substituting it back into the original equation to ensure it satisfies the equality.

It’s important to remember that whatever operation you perform on one side of the equation, you must also perform on the other side to maintain equality.

For example,

 

Clearing Fractions or Eliminating Denominators

You can also solve equations with fractions by first clearing the fractions or eliminating the denominators. You can eliminate the fractions from the equation by multiplying both sides of the equation by a common denominator.

1. Determine the least common denominator (LCD) of the fractions.
2. Multiply both sides of the equation by the LCD.
3. Now that you have eliminated the fractions, solve the equation like you would for any linear equation.

Have a look at this video if you need to review how to solve 2-step equations with fractions using both methods.

• Solve a Two-Step Equation with Fractions

Click on the following worksheet to get a printable pdf document.
Scroll down the page for more Two-Step Equations Worksheets.

 

More Two-Step Equation Worksheets

Printable
(Answers on the second page.)
2-Step Equations Worksheet #1 (fractional coefficients)
2-Step Equations Worksheet #2 (fractional constants)
2-Step Equations Worksheet #3 (fractional coefficients & constants)

Online or Generated
2-Step Equations
Solving 2-Step Equations

Related Lessons & Worksheets

Solve Two-Step Equations
Solve 2-step Equations

More Printable Worksheets

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.