Circle Theorems

Circle theorems are a set of rules that describe the relationships between angles, chords, tangents, and other parts of a circle. They are fundamental concepts in geometry and are often used to solve problems involving circles. Here’s a breakdown of some of the most important circle theorems:

Circle Theorems Summary

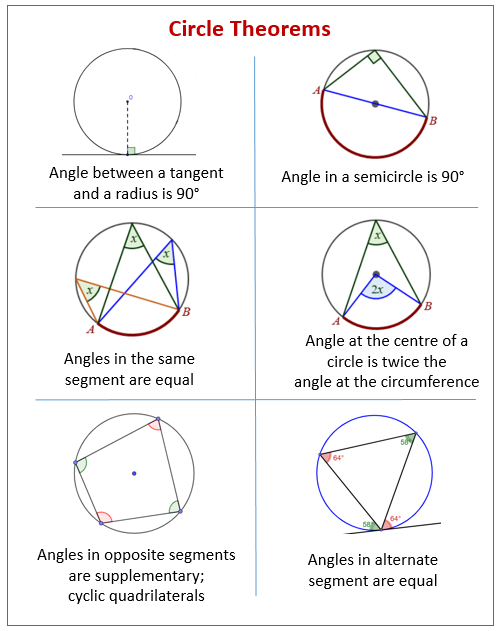
• Angle subtended at the centre of a circle is twice the angle at the circumference.
• The angle between a radius and a tangent is 90 degrees.
• The angle at the centre is twice the angle at the circumference.
• Angles in the same segment are equal.
• The angle in a semi-circle is always 90 degrees.
• The opposite angles in a cyclic quadrilateral always add up to 180 degrees.
• The angle between a circle and a tangent is equal to the angle in the alternate segment.
• The lengths from where two tangents touch a circle to where they meet each other are equal.

The following diagram shows some circle theorems: angle in a semicircle, angle between tangent and radius of a circle, angle at the centre of a circle is twice the angle at the circumference, angles in the same segment are equal, angles in opposite segments are supplementary; cyclic quadrilaterals and alternate segment theorem. Scroll down the page for more examples and solutions of circle theorems.

 

Geometry Worksheets
Practice your skills with the following worksheets:
Printable & Online Geometry Worksheets

Explore Circle Theorems
Explore the theorems interactively by dynamically changing the angles.
Circle Theorems (Interactive)

Here are some of the important circle theorems:

1. Angle at the Centre Theorem:
   The angle subtended by an arc at the centre of a circle is twice the angle subtended by the same arc at any point on the circumference.
   
2. Angle in a Semicircle Theorem:
   An angle inscribed in a semicircle is always a right angle (90°). This is a special case of the Angle at the Centre Theorem where the angle at the centre is 180° (a straight line, the diameter).
   
3. Angles in the Same Segment Theorem:
   Angles subtended by the same arc in the same segment of a circle are equal.
   
4. Cyclic Quadrilateral Theorem:
   The opposite angles in a cyclic quadrilateral (a quadrilateral whose vertices all lie on the circumference of a circle) are supplementary, meaning they add up to 180°.
   
5. Tangent-Radius Theorem:
   A tangent to a circle is perpendicular to the radius drawn to the point of contact. The angle between the tangent and the radius at the point of tangency is always 90°.
   
6. Two Tangents Theorem:
   Tangents drawn from the same external point to a circle are equal in length.
   The line joining the external point to the centre of the circle bisects the angle between the two tangents.
   The line joining the external point to the centre of the circle bisects the angle subtended by the points of contact at the centre.
   
7. Alternate Segment Theorem:
   The angle between a tangent and a chord through the point of contact is equal to the angle in the alternate segment. The alternate segment is the segment of the circle opposite to the angle formed by the tangent and the chord.
   
8. Perpendicular Bisector of a Chord Theorem:
   The perpendicular bisector of a chord always passes through the centre of the circle.
   
9. Equal Chords Subtend Equal Angles at the Centre Theorem:
   Equal chords of a circle subtend equal angles at the centre.
   Conversely, if two chords subtend equal angles at the centre, then the chords are equal.
   
10. Equal Chords are Equidistant from the Centre Theorem:
    Equal chords of a circle are equidistant (equal distance) from the centre.
    Conversely, chords of a circle that are equidistant from the centre are equal in length.

Circle Theorem Basic definitions
Chord, segment, sector, tangent, cyclic quadrilateral.
Theorem: Angle subtended at the centre of a circle is twice the angle at the circumference.

• Show Video Lesson

Circle Theorems part 1 of 2
The angle between a radius and a tangent is 90 degrees.
The angle at the centre is twice the angle at the circumference.
Angles in the same segment are equal.
The angle in a semi-circle is always 90 degrees.
The opposite angles in a cyclic quadrilateral always add up to 180 degrees.

• Show Video Lesson

Circle Theorems part 2 of 2
The angle between a circle and a tangent is equal to the angle in the alternate segment.
The lengths from where two tangents touch a circle to where they meet each other are equal.

• Show Video Lesson

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.