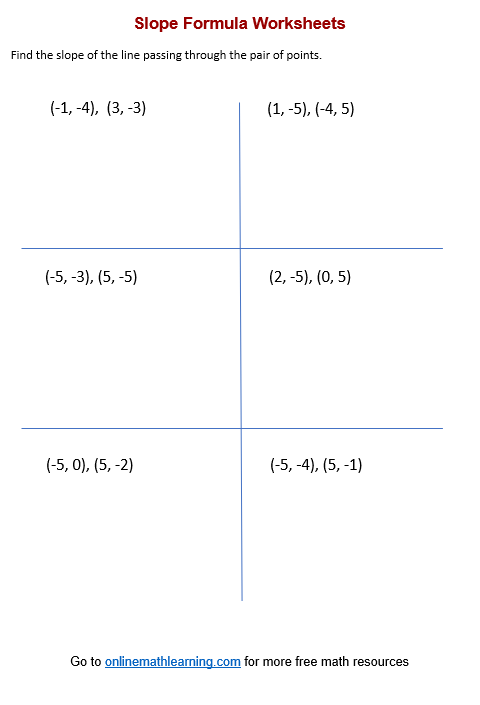
Slope Formula Worksheets

There are six sets of coordinate geometry worksheets:

• Midpoint Formula
  
• Distance Formula
  
• Slope Formula
  
• Standard Form & Slope-Intercept Form
  
• Parallel Lines
  
• Perpendicular Lines
  

Examples, solutions, videos, and worksheets to help grade 7 students learn how to use the slope formula to find the slope of a line passing through two points on the coordinate plane.

How to use the Slope Formula to find the slope of a line passing through two points?

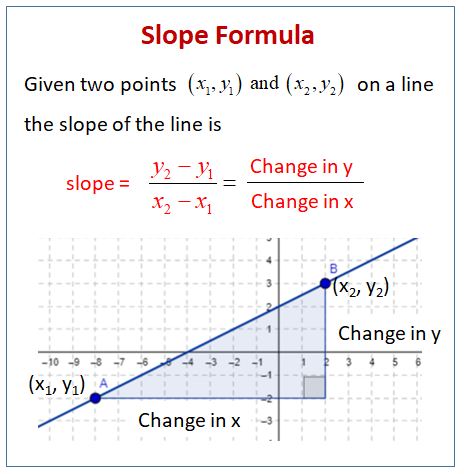
The slope formula is used to calculate the slope of a line that passes through two points in a two-dimensional Cartesian coordinate system (x, y). The slope (m) represents the rate at which the line rises or falls as you move from left to right. The formula for calculating the slope between two points (x₁, y₁) and (x₂, y₂) is as follows:

m = (y₂ - y₁) / (x₂ - x₁)

In this formula:

• (x₁, y₁) are the coordinates of the first point on the line.
• (x₂, y₂) are the coordinates of the second point on the line.
• m is the slope of the line that passes through these two points.

To calculate the slope between two points, you subtract the y-coordinates (vertical change) and divide it by the difference of the x-coordinates (horizontal change) between the two points.

Example:
Use the slope formula to find the slope of the line passing through these two points A(3, 4) and B(6, 8).
m = (8 - 4) / (6 - 3)
m = 4 / 3

So, the slope of the line passing through points A and B is 4/3.

Have a look at this video if you need to review how to use the slope formula.

• How to use the slope formula?

Click on the following worksheet to get a printable pdf document.
Scroll down the page for more Slope Formula Worksheets.

 

More Slope Formula Worksheets

Printable
(Answers on the second page.)
Slope Formula Worksheet #1

Online
Quadrants of Coordinates
Slope of a Line
Slope and Intercept of a Line

Midpoint Formula 1
Midpoint Formula 2

Distance Formula 1
Distance Formula 2

Related Lessons & Worksheets

Slope Formula

More Printable Worksheets

Try out our new and fun Fraction Concoction Game.

Add and subtract fractions to make exciting fraction concoctions following a recipe. There are four levels of difficulty: Easy, medium, hard and insane. Practice the basics of fraction addition and subtraction or challenge yourself with the insane level.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.