Slicing Solids Worksheets

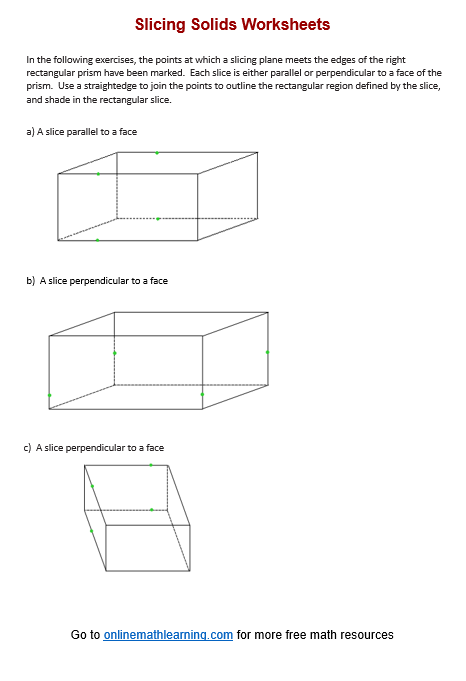
Examples, solutions, videos, and worksheets to help grade 7 students describe rectangular regions that result from slicing a right rectangular prism by a plane perpendicular to one of the faces and describe polygonal regions that result from slicing a right rectangular pyramid by a plane perpendicular to the base and by another plane parallel to the base.

Printable “Solid Shapes” Worksheets:
Nets of Solid Figures
Find Surface Area using Nets
Volume of Rectangular Prisms
Volume of Composite Rectangular Prisms
Slicing Solids

Slicing Solids

Slicing Rectangular Prism
A rectangular prism is a three-dimensional solid with six faces, where each face is a rectangle. The faces are paired, with opposite faces being congruent. A rectangular prism has three dimensions: length (l), width (w), and height (h).

Slicing a rectangular prism refers to cutting the prism along a plane, resulting in a cross-section. The shape of the cross-section depends on the orientation and position of the slice relative to the prism.

Types of Slices in a Rectangular Prism
Horizontal Slice (Parallel to the Base):
The cross-section will be a rectangle that has the same length and width as the base of the prism.
Vertical Slice (Perpendicular to the Base):
If you slice the prism vertically along a plane parallel to one of the sides, the cross-section will be a rectangle.

Slicing Square-based Pyramid
A square-based pyramid is a three-dimensional solid with a square base and four triangular faces that converge at a single point called the apex. The apex is directly above the center of the square base.

Slicing a square-based pyramid refers to cutting the pyramid along a plane, which results in a cross-section. The shape of the cross-section depends on the orientation and position of the slice relative to the pyramid.

Types of Slices in a Square-Based Pyramid
Horizontal Slice (Parallel to the Base):
The cross-section will be a smaller square. The size of this square depends on the height at which the slice is made. The closer the slice is to the base, the larger the square; the closer the slice is to the apex, the smaller the square.
Vertical Slice (Through the Apex):
If the slice passes through the apex and is vertical (perpendicular to the base), the cross-section will be an isosceles triangle. The base of this triangle will be a side of the square base, and the two other sides will correspond to two of the triangular faces of the pyramid.
Vertical Slice (Not Through the Apex):
If the slice is vertical but does not pass through the apex, the cross-section can be a trapezoid. The trapezoid is formed because the slice cuts through two of the triangular faces, creating two parallel sides of different lengths.

Have a look at this video if you need to review how to slice solids.

• Slicing Solids

Click on the following worksheet to get a printable pdf document.
Scroll down the page for more Slicing Solids Worksheets.

 

More Slicing Solids Worksheets

Printable
(Answers on the second page.)
Slicing Solids Worksheet #1 (rectangular prisms)
Slicing Solids Worksheet #2 (rectangular prisms)
Slicing Solids Worksheet #3 (square-based pyramids)

Related Lessons & Worksheets

Slicing a Rectangular Prism
Slicing a Pyramid

More Printable Worksheets

Check out our most popular games!
Fraction Concoction	Fact Family Game	Number Bond Garden
Online Addition Subtraction Game	Penguin Solitaire	Sawayama Solitaire
Ark Solitaire	Eldritch Invasion	Shenzhen Solitaire

Check out more Solitaire games here.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.