Number Properties
In these lessons, we will learn three basic number properties (or laws) that apply to arithmetic operations: Commutative Property, Associative Property and Distributive Property.
Related Pages
Commutative Property
Identity Property Of Addition, Multiplication
More Arithmetic Lessons
Summary of Number Properties
The following table gives a summary of the commutative, associative and distributive properties. Scroll down the page for more examples and explanations of the number properties.
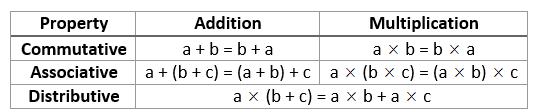
Commutative Property
An operation is commutative if a change in the order of the numbers does not change the results. This means the numbers can be swapped.
Numbers can be added in any order.
For example:
4 + 5 = 5 + 4
x + y = y + x
Numbers can be multiplied in any order.
For example:
5 × 3 = 3 × 5
a × b = b × a
Numbers that are subtracted are NOT commutative.
For example:
4 – 5 ≠ 5 – 4
x – y ≠ y –x
Numbers that are divided are NOT commutative.
For example:
4 ÷ 5 ≠ 5 ÷ 4
x ÷ y ≠ y ÷ x
Associative Property
An operation is associative if a change in grouping does not change the results. This means the parenthesis (or brackets) can be moved.
Numbers that are added can be grouped in any order.
For example:
(4 + 5) + 6 = 5 + (4 + 6)
(x + y) + z = x + (y + z)
Numbers that are multiplied can be grouped in any order.
For example:
(4 × 5) × 6 = 5 × (4 × 6)
(x × y) × z = x × (y × z)
Numbers that are subtracted are NOT associative.
For example:
(4 – 5) – 6 ≠ 4 – (5– 6)
x – y) – z ≠ x – (y – z)
Numbers that are divided are NOT associative.
For example:
(4 ÷ 5) ÷ 6 ≠ 4 ÷ (5÷ 6)
(x ÷ y ) ÷ z ≠ x ÷ ( y ÷ z)
Distributive Property
Distributive property allows you to remove the parenthesis (or brackets) in an expression. Multiply the value outside the brackets with each of the terms in the brackets.
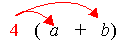
For example:
4(a + b) = 4a + 4b
7(2c – 3d + 5) = 14c – 21d + 35
What happens if you need to multiply (a – 3)(b + 4)?
You do the same thing but with one value at a time.
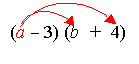
For example:
Multiply a with each term to get a × b + 4 × a = ab + 4a
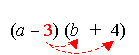
Then, multiply 3 with each term to get “ –3b – 12” (take note of the sign operations).
Put the two results together to get “ab + 4a – 3b – 12”
Therefore, (a – 3)(b + 4) = ab + 4a – 3b – 12
The Commutative Property of addition and multiplication.
The addition of real numbers is commutative.
The multiplication of real numbers is commutative.
The Associative Property of addition and multiplication.
The following video shows more examples of the distributive property.
Associative and Distributive Properties of Multiplication and Addition
A look at the logic behind the associative and distributive properties of multiplication and addition.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.