Rate Distance Time Problems (Opposite Directions)

Distance problems are word problems that involve the distance an object will travel at a certain average rate for a given period of time.

The formula for distance problems is: distance = rate × time or d = r × t.

It would be helpful to use a table to organize the information for distance problems. Make sure that your units are consistent.

The following diagrams give the steps to solve Rate Time Distance Word Problems. Scroll down the page for examples and solutions.

The following diagram gives the steps to solve a Distance-Rate-Time Problem involving two objects going in opposite directions.

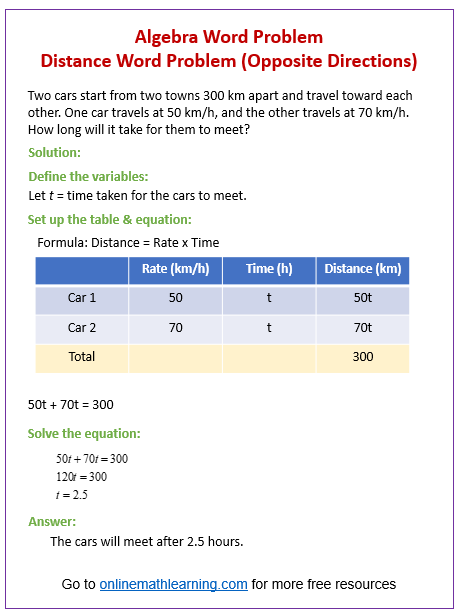
Key Idea for Opposite Direction Problems:

• Total Distance: The sum of the distances traveled by each object equals the initial distance between them (if they are moving towards each other) or the final distance between them (if they are moving away).

Types of Distance Word Problems:
Travel in Same Direction
Travel in Opposite Directions
Round Trip Problems
Average Speed Problems
Wind/Current Problems

Printable & Online Algebra Worksheets

Distance Problems: Traveling In Opposite Directions

Example:
A bus and a car leave the same place and traveled in opposite directions. If the bus is traveling at 50 mph and the car is traveling at 55 mph, in how many hours will they be 210 miles apart?

Solution:
Step 1: Set up a rtd table.

	r	t	d
bus
car

Step 2: Fill in the table with information given in the question.

If the bus is traveling at 50 mph and the car is traveling at 55 mph, in how many hours will they be 210 miles apart?

Let t = time when they are 210 miles apart.

	r	t	d
bus	50	t
car	55	t

Step 3: Fill in the values for d using the formula d = rt

	r	t	d
bus	50	t	50t
car	55	t	55t

Step 4: Since the total distance is 210, we get the equation:

50t + 55t = 210
105t = 210
Isolate variable t

Answer: They will be 210 miles apart in 2 hours.

Example of a distance word problem with vehicles moving in opposite directions

In this video, you will learn to solve introductory distance or motion word problems - for example, cars traveling in opposite directions, bikers traveling toward each other, or one plane overtaking another. You should first draw a diagram to represent the relationship between the distances involved in the problem, then set up a chart based on the formula rate times time = distance.

The chart is then used to set up the equation.

Example:
Two cars leave from the same place at the same time and travel in opposite directions. One car travels at 55 mph and the other at 75 mph. After how many hours will they be 520 miles apart?

• Show Video Lesson

Rate-Time-Distance Problem

Solve this word problem using uniform motion rt = d formula:

Example:
Two cyclists start at the same corner and ride in opposite directions. One cyclist rides twice as fast as the other. In 3 hours, they are 81 miles apart. Find the rate of each cyclist.

• Show Video Lesson

Distance - Opposite Directions

Example:
Brian and Jennifer both leave the convention at the same time traveling in opposite directions. Brian drove at 35 mph and Jennifer drove at 50 mph. After how much time were they 340 miles apart?

• Show Video Lesson

Distance - Opposite Directions find t

Example:
Two joggers start from opposite ends of an 8 mile course running towards each other. One jogger is running at a rate of 4 mph. The other is running at a rate of 6 mph. After how long will the joggers meet?

• Show Video Lesson

Distance - Opposite Directions find r

Example:
Bob and Fred start from the same point and walk in opposite directions. Bob walks 2 mph faster than Fred. After 3 hours they are 30 miles apart. How fast does each walk?

• Show Video Lesson

Check out many other Algebra Word Problems
Age Word Problems, Average Word Problems, Coin Word Problems, Consecutive Integer Word Problems, Digit Word Problems, Distance Word Problems, Fraction Word Problems, Geometry Word Problems, Integer Word Problems, Interest Word Problems, Lever Word Problems, Mixture Word Problems, Money Word Problems, Motion & Distance Word Problems, Number Sequence Word Problems, Proportion Word Problems, Quadratic Equation Word Problems, Ratio Word Problems, Symbol Word Problems, Variation Word Problems, Work Word Problems.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.